题目内容
【题目】如图,在平面直角坐标系中,长方形OABC的顶点O在坐标原点,顶点A、C分别在x、y轴的正半轴上:OA=3,OC=4,D为OC边的中点,E是OA边上的一个动点,当△BDE的周长最小时,E点坐标为_____.
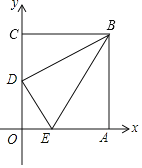
【答案】(1,0)
【解析】
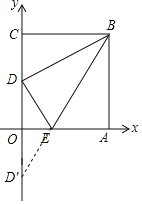
本题是典型的“将军饮马”问题,只需作D关于x轴的对称点D′,连接D′B交x轴于点E,如图,则此时△BDE的周长最小,易得点B和D′坐标,故可利用待定系数法求出直线BD'的解析式,然后求直线BD'与x轴的交点即得答案.
解:如图,作D关于x轴的对称点D′,连接D′B交x轴于点E,连接DE,则DE= D′E,此时△BDE的周长最小,
∵D为CO的中点,∴CD=OD=2,
∵D和D′关于x轴对称,∴D′(0,﹣2),
由题意知:点B(3,4),∴设直线BD'的解析式为y=kx+b,
把B(3,4),D′(0,﹣2)代入解析式,得:![]() ,解得,
,解得,![]() ,
,
∴直线BD'的解析式为y=2x﹣2,
当y=0时,x=1,故E点坐标为(1,0).
故答案为:(1,0).

练习册系列答案
相关题目