题目内容
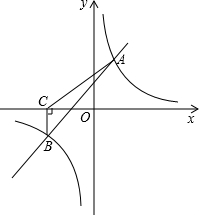
如图,一次函数y=kx+b与反比例函数y=
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,求S△ABC;
(3)连接OA,在x轴上找一点P,使△AOP为等腰三角形,请直接写出点P的坐标.
| m |
| x |
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,求S△ABC;
(3)连接OA,在x轴上找一点P,使△AOP为等腰三角形,请直接写出点P的坐标.

(1)将点A(2,3)代入反比例函数关系式可得:3=
,
解得:m=6,
故可得反比例函数关系式为:y=
,
将点B(-3,n)代入反比例函数关系式可得:n=
=-2,
故点B的坐标为(-3,-2),
将点A、点B的坐标代入一次函数关系式可得:
,
解得:
,
故一次函数解析式为:y=x+1.
(2)
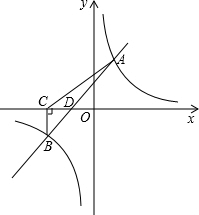
由一次函数解析式为y=x+1,可得点D的坐标为(-1,0),
则OD=1,CD=OC-OD=2,
则S△ABC=S△BCD+S△ACD=
CD×|B纵|+
CD×|A纵|=2+3=5.
(3)
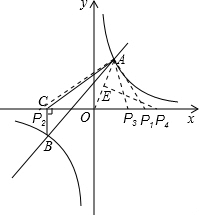
①若OA=OP,
此时点P位于P1或P2,则可得P1(
,0),P2(-
,0);
②若OA=AP,
此时点P位于P3,则可得P3(4,0);
③若OP=AP,作OA的中垂线,交x轴与P4,则此时点P位于P4,
此时OE=
OA=
,
根据点A的坐标可得:cos∠AOP4=
=
,
则
=
,
解得:OP4=
,
则点P4的坐标为(
,0).
综上可得点P的坐标为P1(
,0)或P2(-
,0)或P3(4,0)或(
,0).
| m |
| 2 |
解得:m=6,
故可得反比例函数关系式为:y=
| 6 |
| x |
将点B(-3,n)代入反比例函数关系式可得:n=
| 6 |
| -3 |
故点B的坐标为(-3,-2),
将点A、点B的坐标代入一次函数关系式可得:
|
解得:
|
故一次函数解析式为:y=x+1.
(2)

由一次函数解析式为y=x+1,可得点D的坐标为(-1,0),
则OD=1,CD=OC-OD=2,
则S△ABC=S△BCD+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)

①若OA=OP,
此时点P位于P1或P2,则可得P1(
| 13 |
| 13 |
②若OA=AP,
此时点P位于P3,则可得P3(4,0);
③若OP=AP,作OA的中垂线,交x轴与P4,则此时点P位于P4,
此时OE=
| 1 |
| 2 |
| ||
| 2 |
根据点A的坐标可得:cos∠AOP4=
| A横 |
| OA |
2
| ||
| 13 |
则
| OE |
| OP4 |
2
| ||
| 13 |
解得:OP4=
| 13 |
| 4 |
则点P4的坐标为(
| 13 |
| 4 |
综上可得点P的坐标为P1(
| 13 |
| 13 |
| 13 |
| 4 |

练习册系列答案
相关题目
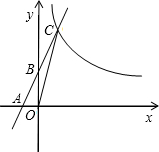 内交于点C,且S△AOC=6.
内交于点C,且S△AOC=6.