题目内容
矩形ABCD中，对角线AC、BD交于点O，AE⊥BD于E，若
，AE=
，则BD= ．
，AE=，则BD= ．4或
如图（一）所示，
AB是矩形较短边时，
∵矩形ABCD，
∴OA=OD=
BD；
∵OE：ED=1：3，
∴可设OE=x，ED=3x，则OD=2x
∵AE⊥BD，AE=
，
∴在Rt△OEA中，x2+（）2=（2x）2，
∴x=1
∴BD=4．
当AB是矩形较长边时，如图（二）所示，
∵OE：ED=1：3，
∴设OE=x，则ED=3x，
∵OA=OD，
∴OA=4x，
在Rt△AOE中，x2+（）2=（4x）2，
∴x=
，
∴BD=8x=8×=
．
AB是矩形较短边时，
∵矩形ABCD，
∴OA=OD=
BD；∵OE：ED=1：3，
∴可设OE=x，ED=3x，则OD=2x
∵AE⊥BD，AE=
，∴在Rt△OEA中，x2+（
）2=（2x）2，∴x=1
∴BD=4．
当AB是矩形较长边时，如图（二）所示，
∵OE：ED=1：3，
∴设OE=x，则ED=3x，
∵OA=OD，
∴OA=4x，
在Rt△AOE中，x2+（
）2=（4x）2，∴x=
，∴BD=8x=8×
=．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
中，点
分别为边
的中点，
相交于点
，则可得结论：①
；②
．（不需要证明）
，则上面的结论①，②是否仍然成立？（请直接回答“成立”或“不成立”）
的延长线和
的延长线上，且
和
，若点
分别为
的中点，请判断四边形
是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程．
中，
，
，
，
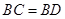，则
（ ）
