Question

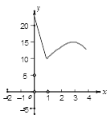
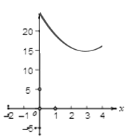
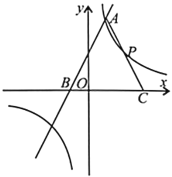
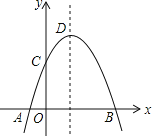
【题目】如图，抛物线y＝﹣x2+2x+c+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个命题：

①抛物线的对称轴是直线x＝1；

②若OC＝OB，则c＝2；

③若M（x0，y0）是x轴上方抛物线上一点，则（x0﹣a）（x0﹣b）＜0；

④抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2．其中真命题个数是（　　）

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

根据二次函数的对称轴、二次函数图象上点的坐标特征、二次函数的性质判断即可．

解：①抛物线的对称轴是直线x＝﹣＝1，本说法是真命题；

②当x＝0时，y＝c+1，即点C的坐标为（0，c+1），

∴OC＝1，

当OB＝OC＝c+1时，点B的坐标为（c+1，0），

∴0＝﹣（c+1）2+2（c+1）+c+1，

解得，c1＝﹣1（舍去），c2＝2，本说法是真命题；

③抛物线y＝﹣x2+2x+c+1交x轴于点A（a，0）和B（b，0），

∴a+b＝2，ab＝c+1，

∵M（x0，y0）是抛物线x轴上方一点，

∴x02＜2x0+c+1，

∴（x0﹣a）（x0﹣b）＝x02﹣（a+b）x0+ab＜2x0+c+1﹣2x0+c+1＝0，本说法是真命题；

④因为x1＜1＜x2，所以点P和Q在对称轴两侧，而x1+x2＞2，则点Q比点P离对称轴的距离要大，所以y1＞y2，本说法是真命题；

故选：D