题目内容
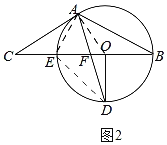
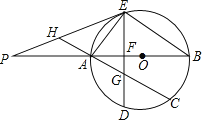
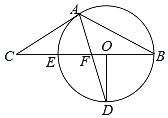
【题目】如图，在△ABC中，AC＝AB，点E在BC上，以BE为直径的⊙O经过点A，点D是直径BE下方半圆的中点，AD交BC于点F，且∠B＝2∠D．
（1）求∠B的度数；
（2）求证：AC为⊙O的切线；
（3）连接DE，若OD＝3，求
的值．
【答案】（1）∠B＝30°；（2）详见解析；（3）
．
【解析】
（1）先判断出∠BAO+∠DAO＝45°，再判断出∠DAO＝∠D，∠BAO＝∠B，即可得出结论；
（2）先求出∠C＝30°，∠AOC＝60°，即可得出结论；
（3）先求出AE＝3，再计算出CF，进而求出EF，最后判断出△DEF∽△DAE，即可得出结论．
解：（1）如图1，连接OA，
∵点D是直径BE下方半圆的中点，
∴
，
∴∠BOD＝∠EOD＝90°，
∴∠BAD＝
∠BOD＝45°，
∴∠BAO+∠DAO＝45°，
∵OA＝OB＝OD，
∴∠DAO＝∠D，∠BAO＝∠B，
∴∠B+∠D＝45°，
∵∠B＝2∠D，
∴∠B＝30°；
（2）由（1）知，∠B＝30°，
∵AC＝AB，
∴∠C＝∠B＝30°，
∴∠AOC＝2∠B＝60°，
∴∠CAO＝180°﹣∠C﹣∠CAO＝90°，
∵OA为⊙O的半径，
∴AC为⊙O的切线；
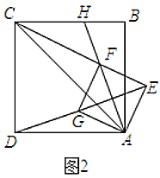
（3）如图2，连接OA，AE，则∠BAE＝90°，
在Rt△ACO中，∠CAO＝90°，∠C＝30°，AO＝OE＝DO＝3，
∴AC=
AO=3，OC＝2AO＝6，
∴CE＝OC﹣OE＝3，
∴CE＝OE＝3，
由（2）知，∠CAO＝90°，
∴AE＝OC＝3，
∵∠CAO＝∠COD＝90°，∠OAD＝∠ODA＝∠B＝15°，
∴∠CAF＝∠OFD＝75°，
∵∠CFA＝∠OFD，
∴∠CAF＝∠CFA，
∴CF＝AC＝3，
∴EF=CF-CE=3
连接DE，
∴∠DEF＝∠BAD＝45°，
∴∠DAE＝∠BAE﹣∠BAD＝45°，
∴∠DEF＝∠DAE，
∵∠EDF＝∠ADE，
∴△EDF∽△ADE，
∴
．
