题目内容
【题目】如图,在Rt△DEF中,∠EFD=90°,∠DEF=30°,EF=3cm,边长为2cm的等边△ABC的顶点C与点E重合,另一个顶点B(在点C的左侧)在射线FE上.将△ABC沿EF方向进行平移,直到A、D、F在同一条直线上时停止,设△ABC在平移过程中与△DEF的重叠面积为ycm2,CE的长为xcm,则下列图象中,能表示y与x的函数关系的图象大致是( )
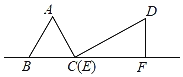
A. B.
B.
C.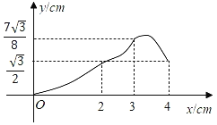 D.
D.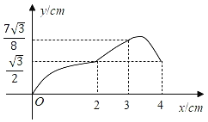
【答案】A
【解析】
分0≤x≤2、2<x≤3、3<x≤4三种情况,分别求出函数表达式即可求解.
解:①当0≤x≤2时,如图1,
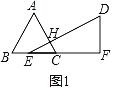
设AC交ED于点H,则EC=x,
∵∠ACB=60°,∠DEF=30°,
∴∠EHC=90°,
y=S△EHC=![]() ×EH×HC=
×EH×HC=![]() ECsin∠ACB×EC×cos∠ACB=
ECsin∠ACB×EC×cos∠ACB=![]() CE2=
CE2=![]() x2,
x2,
该函数为开口向上的抛物线,当x=2时,y=![]() ;
;
②当2<x≤3时,如图2,
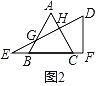
设AC交DE于点H,AB交DE于点G,
同理△AHG为以∠AHG为直角的直角三角形,
EC=x,EB=x﹣2=BG,则AG=2﹣BG=2﹣(x﹣2)=4﹣x,
边长为2的等边三角形的面积为:![]() 2×
2×![]() =
=![]() ;
;
同理S△AHG=![]() (4﹣x)2,
(4﹣x)2,
y=S四边形BCHG=S△ABC﹣S△AHG=![]() ﹣
﹣![]() (x﹣4)2,
(x﹣4)2,
函数为开口向下的抛物线,当x=3时,y=![]() ,
,
③当3<x≤4时,如图3,
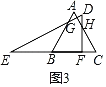
同理可得:y=![]() ﹣[
﹣[![]() (4﹣x)2+
(4﹣x)2+![]() (x﹣3)2]=﹣
(x﹣3)2]=﹣![]() x2+4
x2+4![]() x﹣
x﹣![]() ,
,
函数为开口向下的抛物线,当x=4时,y=![]() ;
;
故选:A.

练习册系列答案
相关题目