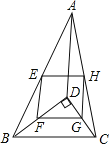题目内容
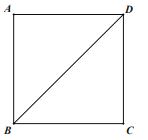
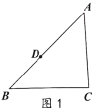
【题目】将矩形ABCD沿对角线BD翻折,点A落在点A′处,AD交BC于点E,点F在CD上,连接EF,且CE=3CF,如图1.
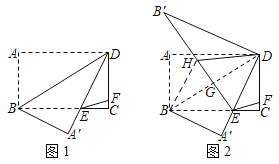
(1)试判断△BDE的形状,并说明理由;
(2)若∠DEF=45°,求tan∠CDE的值;
(3)在(2)的条件下,点G在BD上,且不与B、D两点重合,连接EG并延长到点H,使得EH=BE,连接BH、DH,将△BDH沿DH翻折,点B的对应点B′恰好落在EH的延长线上,如图2.当BH=8时,求GH的长.
【答案】(1)△BDE是等腰三角形;理由见解析;(2)tan∠CDE=![]() ;(3)GH=
;(3)GH=![]() .
.
【解析】
(1)根据折叠的性质和平行线的性质得:![]() ,由等角对等边可得
,由等角对等边可得![]() 是等腰三角形;
是等腰三角形;
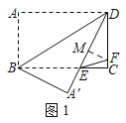
(2)如图1,过点![]() 作
作![]() 于
于![]() ,根据等腰直角三角形的性质得:
,根据等腰直角三角形的性质得:![]() ,设
,设![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() ,
,![]() ,设
,设![]() ,根据三角函数定义可得
,根据三角函数定义可得![]() ,最后利用勾股定理列方程可得
,最后利用勾股定理列方程可得![]() 与
与![]() 的关系,从而得结论;
的关系,从而得结论;
(3)如图2,作辅助线,构建全等三角形,证明![]() ,得
,得![]() ,从而由等腰三角形三线合一的性质得
,从而由等腰三角形三线合一的性质得![]() ,证明
,证明![]() ,列比例式可得结论.
,列比例式可得结论.
解:(1)![]() 是等腰三角形,
是等腰三角形,
理由是:如图1,![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
由折叠得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形;
是等腰三角形;
(2)如图1,过点![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() 设
设![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() (舍
(舍![]() ,
,
![]() ;
;
(3)如图2,过点![]() 作
作![]() ,
,
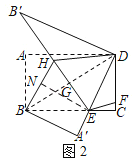
由折叠得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
由(2)知:![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目