题目内容
【题目】已知抛物线与![]() 轴交于点
轴交于点![]() 和
和![]() 且过点
且过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 抛物线的顶点坐标;
抛物线的顶点坐标;
![]()
![]() 取什么值时,
取什么值时,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 取什么值时,
取什么值时,![]() 随
随![]() 增大而减小.
增大而减小.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 随
随![]() 增大而增大;当
增大而增大;当![]() 时,
时,![]() 随
随![]() 增大而减小.
增大而减小.
【解析】
(1)设二次函数解析式为y=a(x﹣1)(x﹣2),然后把点(3,4)代入函数解析式求得a的值即可;
(2)将(1)中抛物线的解析式利用配方法转化为顶点式,可以直接写出顶点坐标;
(3)根据抛物线的开口方向和对称轴写出答案.
(1)∵二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),
∴设该二次函数解析式为y=a(x﹣1)(x﹣2)(a≠0),
把点(3,4)代入,得:
a×(3﹣1)×(3﹣2)=4,
解得:a=2.
则该抛物线的解析式为:y=2(x﹣1)(x﹣2);
(2)由(1)知,抛物线的解析式为y=2(x﹣1)(x﹣2).
∵y=2(x﹣1)(x﹣2)=2(x![]() )2
)2![]() ,
,
∴该抛物线的顶点坐标是:(![]() ,
,![]() ).
).
(3)由抛物线的解析式y=2(x![]() )2
)2![]() 知,抛物线开口方向向上,对称轴是x
知,抛物线开口方向向上,对称轴是x![]() .
.
结合二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),作出该抛物线的大致图象.
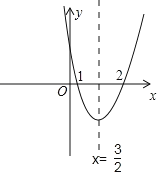
如图所示,当x![]() 时,y随x的增大而增大;当x
时,y随x的增大而增大;当x![]() 时,y随x的增大而减小.
时,y随x的增大而减小.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目