题目内容
【题目】（1）先化简，再求值：
其中，a是方程x2+3x+1＝0的根．
（2）已知抛物线y＝ax2+bx+c的对称轴为x＝2，且经过点（1，4）和（5，0），试求该抛物线的表达式．
【答案】（1）
，
；（2）y＝﹣
x2+2x+
．
【解析】
（1）先把分子分母能因式分解的进行因式分解，然后进行计算化简，再根据一元二次方程解的定义求出a2+3a＝－1，整体代入即可；
（2）利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为（1，0），于是可设抛物线的解析式为y＝a（x＋1）（x5），然后把（1，4）代入求出a即可．
（1）原式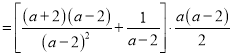
，
∵a是方程x2+3x+1＝0的根，
∴a2+3a+1＝0，即a2+3a＝－1，
原式＝；
（2）∵抛物线的对称轴为直线x＝2，抛物线与x轴的一个交点坐标为（5，0），
∴抛物线与x轴的另一个交点坐标为（﹣1，0），
∴设抛物线的解析式为y＝a（x+1）（x﹣5），
把（1，4）代入得4＝a×2×（﹣4），
解得a＝，
∴抛物线的解析式为y＝（x+1）（x﹣5）＝
．
练习册系列答案
相关题目
