Question

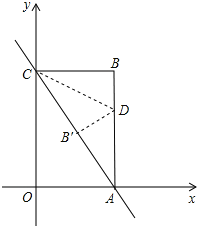
【题目】在四边形OABC中，CB∥OA，∠COA=90°，CB=3，OA=6，BA=3．分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系．

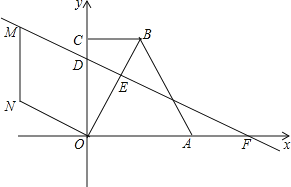
（1）求点B的坐标；

（2）已知D、E分别为线段OC、OB上的点，OD=5，OE=2EB，直线DE交x轴于点F．求直线DE的解析式；

（3）点M在（2）中直线DE上，四边形ODMN是菱形，求N的坐标．

Answer 1

【答案】（1）点B的坐标为（3，6）；（2）y=﹣x+5；（3）N的坐标为（﹣2，）．

【解析】

试题分析：（1）作BH⊥OA于H，根据矩形的性质求出OH的长，根据勾股定理求出BH的长，得到点B的坐标；

（2）作EG⊥OA于G，得到△OGE∽△OHB，根据题意和相似三角形的性质求出点E、D的坐标，运用待定系数法求出直线DE的解析式；

（3）作MP⊥y轴于点P，得到△MPD∽△FOD，根据相似三角形的性质和勾股定理计算即可．

解：如图1，作BH⊥OA于H，则四边形OHBC为矩形，

∴OH=CB=3，

∴AH=OA﹣OH=3，

∴BH==6，

∴点B的坐标为（3，6）；

（2）如图1，作EG⊥OA于G，则EG∥BH，

∴△OGE∽△OHB，

∴==，

∵OE=2EB，

∴=，又OH=3，BH=6，

∴OG=2，EG=4，

∴点E的坐标为（2，4），

∵OC=BH=6，OD=5，

∴点D的坐标为（0，5），

设直线DE的解析式为y=kx+b，

∴，

解得，，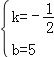

∴直线DE的解析式为y=﹣x+5；

（3）如图2，作MP⊥y轴于点P，

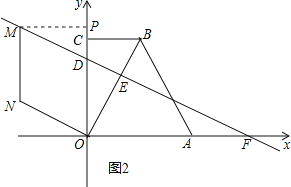
∵四边形ODMN是菱形，

∴DM=MN=NO=OD=5，

∵MP∥OA，

∴△MPD∽△FOD，

∴==，

当y=0，即﹣x+5=0时，x=10，

∴点F的坐标为（0，10），

∴DF==5，

∴==，

解得，MP=2，PD=，

∴OP=5+，

∴N的坐标为（﹣2，）．