Question

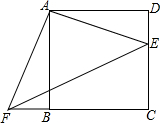四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
（1）试判断△AEF的形状，并说明理由；
（2）填空：△ABF可以由△ADE绕旋转中心

A

 点，按顺时针方向旋转

90

度得到；
（3）若BC=8，则四边形AECF的面积为

64

．（直接写结果）

Answer 1

分析：（1）根据正方形性质得出AB=AD，∠DAB=∠ABF=∠D=90°，证△ADE≌△ABF，推出AE=AF，∠DAE=∠FAB即可．
（2）根据全等三角形性质和旋转的性质得出即可．
（3）求出四边形AECF的面积等于正方形ABCD面积，求出正方形的面积即可．

解答：解：（1）△AEF是等腰直角三角形，
理由是：∵四边形ABCD是正方形，F是BC延长线上一点，
∴AB=AD，∠DAB=∠ABF=∠D=90°，
在△ADE和△ABF中，

AD=AB ∠D=∠ABF DE=BF

，
∴△ADE≌△ABF（SAS）
∴AE=AF，∠DAE=∠FAB，
∵∠DAB=∠DAE+∠BAE=90°，
∴∠FAE=∠DAB=90°，
即△AEF是等腰直角三角形．

（2）△ABF可以由△ADE绕旋转中心A点，按顺时针方向旋转90°得到的，
故答案为：A，90．

（3）∵△ADE≌△ABF，
∴S_ADE=S_△ABF，
∴四边形AECF的面积S=S_{四边形ABCE}+S_△ABF
=S_{四边形ABCE}+S_△ADE
=S_{正方形ABCD}
=8×8
=64，
故答案为：64．

点评：本题考查了旋转性质，全等三角形的性质和判定，正方形性质的应用，主要考查学生的推理能力．