题目内容
课题学习:
(1)如图1,E、F、G、H分别是正方形ABCD各边的中点,则四边形EFGH是
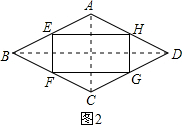
(2)如图2,E、F、G、H分别是菱形ABCD各边的中点,则四边形EFGH是
(3)如图3,梯形ABCD中,AD∥BC,对角线AC⊥BD,垂足为O,E、F、G、H分别为各边的中点.四边形EFGH是
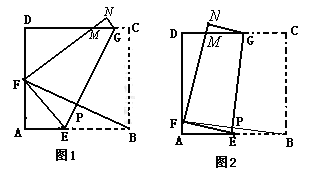
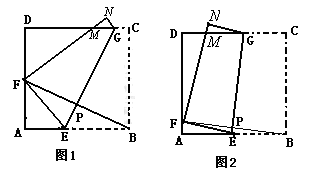
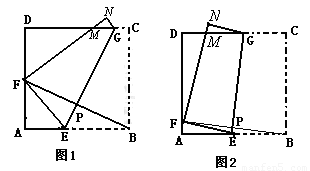
(4)如图4,E、G分别是平行四边形ABCD的边AB、DC的中点,H、F分别是边形AD、BC上的点,且四边形EFGH为平行四边形,若把平行四边形ABCD的面积记为S1,把平行四边形形EFGH的面积记为S2,试猜想S1和S2间的数量关系,并加以证明.

(1)如图1,E、F、G、H分别是正方形ABCD各边的中点,则四边形EFGH是
正方
正方
形,正方形ABCD的面积记为S1,EFGH的面积为S2,则S1和S2间的数量关系:S1=2S2
S1=2S2
;(2)如图2,E、F、G、H分别是菱形ABCD各边的中点,则四边形EFGH是
矩
矩
形,菱形ABCD的面积为S1,EFGH的面积为S2,则S1和S2间的数量关系:S1=2S2
S1=2S2
;(3)如图3,梯形ABCD中,AD∥BC,对角线AC⊥BD,垂足为O,E、F、G、H分别为各边的中点.四边形EFGH是
矩
矩
形;若梯形ABCD的面积记为S1,四边形EFGH的面积记为S2,由图可猜想S1和S2间的数量关系为:S1=2S2
S1=2S2
;(4)如图4,E、G分别是平行四边形ABCD的边AB、DC的中点,H、F分别是边形AD、BC上的点,且四边形EFGH为平行四边形,若把平行四边形ABCD的面积记为S1,把平行四边形形EFGH的面积记为S2,试猜想S1和S2间的数量关系,并加以证明.

分析:(1)连接AC、BD.先根据三角形中位线的性质得出EH∥BD∥FG,EF∥AC∥HG,EH=FG=
BD,EF=HG=
AC,则四边形EFGH为平行四边形,再由正方形的对角线相等且互相垂直,得出EF=FG,EF⊥FG,从而证明?EFGH是正方形;利用相似多边形的面积比等于相似比的平方可求得S1=2S2;
(2)连接AC、BD.先根据三角形中位线的性质得出EH∥BD∥FG,EF∥AC∥HG,EH=FG=
BD,EF=HG=
AC,则四边形EFGH为平行四边形,再由菱形的对角线互相垂直,得出EF⊥FG,从而证明?EFGH是矩形;利用相似三角形的面积比等于相似比的平方可求得S1=2S2;
(3)先根据三角形中位线的性质得出EH∥BD∥FG,EF∥AC∥HG,EH=FG=
BD,EF=HG=
AC,则四边形EFGH为平行四边形,再由AC⊥BD,得出EF⊥FG,从而证明?EFGH是矩形;利用相似多边形的面积比等于相似比的平方可求得S1=2S2;
(4)过点H作HM⊥AB于M,延长MH交CD于N,先由垂线的唯一性得出MN为平行四边形ABCD的边AB、DC上的高,再根据三角形的面积公式得出S△AEH+S△DHG=
AB•MN=
S?ABCD,同理得出S△BEF+S△CFG=
AB•PQ=
S?ABCD,进而求出S?EFGH=
S?ABCD,即S1=2S2.
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接AC、BD.先根据三角形中位线的性质得出EH∥BD∥FG,EF∥AC∥HG,EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
(3)先根据三角形中位线的性质得出EH∥BD∥FG,EF∥AC∥HG,EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
(4)过点H作HM⊥AB于M,延长MH交CD于N,先由垂线的唯一性得出MN为平行四边形ABCD的边AB、DC上的高,再根据三角形的面积公式得出S△AEH+S△DHG=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
解答: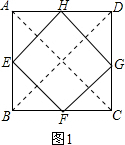 解:(1)如图1.连接AC、BD.
解:(1)如图1.连接AC、BD.
∵E、F、G、H分别是正方形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=
BD,EF=HG=
AC,
∴四边形EFGH为平行四边形,
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴EF=FG,EF⊥FG,
∴?EFGH是正方形;
∵正方形ABCD∽正方形EFGH,
∴S1:S2=(AB:EF)2=(2BE:
BE)2=(2:
)2=2,
∴S1=2S2;
 (2)如图2.连接AC、BD.
(2)如图2.连接AC、BD.
∵E、F、G、H分别是菱形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=
BD,EF=HG=
AC,
∴四边形EFGH为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴EF⊥FG,
∴?EFGH是矩形;
在△ABD中,∵EH∥BD,
∴△AEH∽△ABD,
∵EH=
BD,
∴S△AEH:S△ABD=(EH:BD)2=
,即S△AEH=
S△ABD,
同理可证:S△CFG=
S△CBD,
∴S△AEH+S△CFG=
(S△ABD+S△CBD)=
S菱形ABCD.
同理可得S△BEF+S△DHG=
(S△ABC+S△CDA)=
S菱形ABCD,
∴S△AEH+S△CFG+S△BEF+S△DHG=
S菱形ABCD,
∴S矩形EFGH=S菱形ABCD-(S△AEH+S△CFG+S△BEF+S△DHG)=
S菱形ABCD,
∴S1=2S2;
(3)如题目图3.∵E、F、G、H分别是梯形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=
BD,EF=HG=
AC,
∴四边形EFGH为平行四边形,
∵AC⊥BD,
∴EF⊥FG,
∴?EFGH是矩形;
在△ABD中,∵EH∥BD,
∴△AEH∽△ABD,
∵EH=
BD,
∴S△AEH:S△ABD=(EH:BD)2=
,即S△AEH=
S△ABD,
同理可证:S△CFG=
S△CBD,
∴S△AEH+S△CFG=
(S△ABD+S△CBD)=
S梯形ABCD.
同理可得S△BEF+S△DHG=
(S△ABC+S△CDA)=
S梯形ABCD,
∴S△AEH+S△CFG+S△BEF+S△DHG=
S梯形ABCD,
∴S矩形EFGH=S梯形ABCD-(S△AEH+S△CFG+S△BEF+S△DHG)=
S梯形ABCD,
∴S1=2S2;
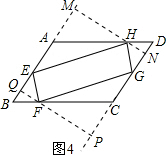 (4)S1=2S2.理由如下:
(4)S1=2S2.理由如下:
如图4.过点H作HM⊥AB于M,延长MH交CD于N.
∵AB∥CD,HM⊥AB,
∴HM⊥CD,即MN⊥CD,则MN为平行四边形ABCD的边AB、DC上的高.
∵E、G分别是平行四边形ABCD的边AB、DC的中点,
∴AE=BE=CG=GD=
AB=
CD.
∵S△AEH=
AE•HM=
AB•HM,S△DHG=
GD•HN=
CD•HN,
∴S△AEH+S△DHG=
AB•HM+
CD•HN=
AB(HM+HN)=
AB•MN=
S?ABCD.
同理可得S△BEF+S△CFG=
AB•FQ+
CD•FP=
AB(FQ+FP)=
AB•PQ=
S?ABCD,
∴S△AEH+S△CFG+S△BEF+S△DHG=
S?ABCD,
∴S?EFGH=S?ABCD-(S△AEH+S△CFG+S△BEF+S△DHG)=
S?ABCD,
∴S1=2S2.
 解:(1)如图1.连接AC、BD.
解:(1)如图1.连接AC、BD.∵E、F、G、H分别是正方形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH为平行四边形,
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴EF=FG,EF⊥FG,
∴?EFGH是正方形;
∵正方形ABCD∽正方形EFGH,
∴S1:S2=(AB:EF)2=(2BE:
| 2 |
| 2 |
∴S1=2S2;
 (2)如图2.连接AC、BD.
(2)如图2.连接AC、BD.∵E、F、G、H分别是菱形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴EF⊥FG,
∴?EFGH是矩形;
在△ABD中,∵EH∥BD,
∴△AEH∽△ABD,
∵EH=
| 1 |
| 2 |
∴S△AEH:S△ABD=(EH:BD)2=
| 1 |
| 4 |
| 1 |
| 4 |
同理可证:S△CFG=
| 1 |
| 4 |
∴S△AEH+S△CFG=
| 1 |
| 4 |
| 1 |
| 4 |
同理可得S△BEF+S△DHG=
| 1 |
| 4 |
| 1 |
| 4 |
∴S△AEH+S△CFG+S△BEF+S△DHG=
| 1 |
| 2 |
∴S矩形EFGH=S菱形ABCD-(S△AEH+S△CFG+S△BEF+S△DHG)=
| 1 |
| 2 |
∴S1=2S2;
(3)如题目图3.∵E、F、G、H分别是梯形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH为平行四边形,
∵AC⊥BD,
∴EF⊥FG,
∴?EFGH是矩形;
在△ABD中,∵EH∥BD,
∴△AEH∽△ABD,
∵EH=
| 1 |
| 2 |
∴S△AEH:S△ABD=(EH:BD)2=
| 1 |
| 4 |
| 1 |
| 4 |
同理可证:S△CFG=
| 1 |
| 4 |
∴S△AEH+S△CFG=
| 1 |
| 4 |
| 1 |
| 4 |
同理可得S△BEF+S△DHG=
| 1 |
| 4 |
| 1 |
| 4 |
∴S△AEH+S△CFG+S△BEF+S△DHG=
| 1 |
| 2 |
∴S矩形EFGH=S梯形ABCD-(S△AEH+S△CFG+S△BEF+S△DHG)=
| 1 |
| 2 |
∴S1=2S2;
 (4)S1=2S2.理由如下:
(4)S1=2S2.理由如下:如图4.过点H作HM⊥AB于M,延长MH交CD于N.
∵AB∥CD,HM⊥AB,
∴HM⊥CD,即MN⊥CD,则MN为平行四边形ABCD的边AB、DC上的高.
∵E、G分别是平行四边形ABCD的边AB、DC的中点,
∴AE=BE=CG=GD=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△AEH=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴S△AEH+S△DHG=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
同理可得S△BEF+S△CFG=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴S△AEH+S△CFG+S△BEF+S△DHG=
| 1 |
| 2 |
∴S?EFGH=S?ABCD-(S△AEH+S△CFG+S△BEF+S△DHG)=
| 1 |
| 2 |
∴S1=2S2.
点评:本题考查了三角形中位线的性质,特殊四边形的判定和性质,相似多边形的性质,多边形的面积,综合性较强,有一定难度.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目