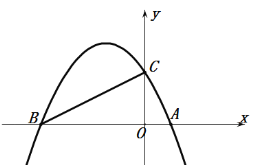题目内容
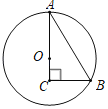
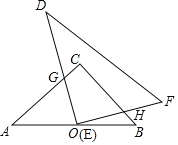
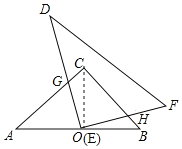
【题目】如图,在等腰直角三角形ABC中,∠C=90°,AB=8![]() ,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
(1)当点G在AC边什么位置时,四边形CGOH是正方形.
(2)等腰直角三角ABC的边被Rt△DEF覆盖部分的两条线段CG与CH的长度之和是否会发生变化,如不发生变化,请求出CG与CH之和的值:如发生变化,请说明理由.
【答案】(1)点G在AC的中点时,四边形CGOH是正方形;(2)CG与CH的和不会发生变化,CG+CH=8.
【解析】
(1)由三角形中位线定理可得OG∥BC,OG=![]() BC,可证四边形CGOH是矩形,由等腰直角三角形的性质可得∠ACO=∠COG=45°,可得CG=GO,可得结论;
BC,可证四边形CGOH是矩形,由等腰直角三角形的性质可得∠ACO=∠COG=45°,可得CG=GO,可得结论;
(2)由“ASA”可证△GOC≌△HOB,可得CG=BH,即可得CG+CH=HB+CH=BC=8.
解:(1)当点G在AC的中点时,四边形CGOH是正方形,
连接CO,
∵O为AB的中点,点G是AC中点,
∴OG∥BC,OG=![]() BC,
BC,
∴∠CGO=∠C=90°,
∵∠GOF=90°,
∴四边形CGOH是矩形,
∵AC=BC,∠ACB=90°,AO=BO,
∴∠ACO=45°,且∠CGO=90°,
∴∠ACO=∠COG=45°,
∴CG=GO,
∴矩形CGOH是正方形;
(2)CG与CH的和不会发生变化,
理由如下:
连接OC,
∵△ABC是等腰直角三角形且点O为中点
∴∠GCO=∠B=45°,∠COB=90°,CO=BO
∵∠DOF=90°=∠COB,
∴∠GOC=∠HOB,且CO=BO,∠GCO=∠B=45°,
∴△GOC≌△HOB(ASA)
∴HB=GC,
∴CG+CH=HB+CH=BC
∵AB=8![]() ,
,
∴BC=AC=8
∴CG+CH=8.

【题目】在平面直角坐标系xOy中,抛物线C1:y=﹣x2+2x.
(1)补全表格:
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
y=﹣x2+2x | (1,1) |
|
| (0,0) |
(2)将抛物线C1向上平移3个单位得到抛物线C2,请画出抛物线C1,C2,并直接回答:抛物线C2与x轴的两交点之间的距离是抛物线C1与x轴的两交点之间距离的多少倍.