题目内容
【题目】如图，已知抛物线y＝
x+2与x轴交于A、B两点，交y轴于点C．
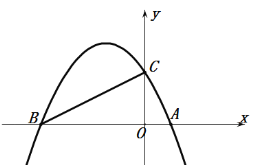
（1）判断△ABC的形状，并说明理由．
（2）在抛物线对称轴上是否存在一点P，使得以A、C、P为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，说明理由．
【答案】（1）直角三角形，理由见解析；（2）存在，点P的坐标（﹣
，0），（﹣，2+
），（﹣，2﹣）．
【解析】
（1）由二次函数图象上点的坐标特征求得点A、B、C的坐标，易得△ABC三边的长度，由勾股定理逆定理可以判定△ABC是直角三角形；
（2）该题中没有指出等腰三角形的底边，所用需要分类讨论：以AP为腰和以AP为底边两种情况，根据两点间的距离公式列出方程，通过解方程求得符合条件点P的坐标即可．
（1）直角三角形，理由如下：
当y＝0时，﹣
x2﹣x+2＝0，解得，x1＝﹣4，x2＝1，
即B（﹣4，0），A（1，0）．
当x＝0时，y＝2，即C（0，2）．
AB＝1﹣（﹣4）＝5，AB2＝25，
AC2＝（1﹣0）2+（0﹣2）2＝5，
BC2＝（﹣4﹣0）2+（0﹣2）2＝20，
∵AC2+BC2＝AB2，
∴△ABC是直角三角形；
（2）存在，理由如下：
y＝﹣x2﹣x+2的对称轴是x＝﹣，设P（﹣，n），
PA2＝（1+）2+n2＝
+n2，PC2＝
+（2﹣n）2，AC2＝5．
分类讨论：
①当AP＝AC时，AP2＝AC2，
+n2＝5，方程无解； 不存在．
②当PA＝PC时，PA2＝PC2，
+n2＝+（2﹣n）2，
解得，n＝0，即P1（﹣，0）；
③当CA＝CP时CA2＝CP2，+（2﹣n）2＝5，
解得，n1＝2+，n2＝2﹣，
故P2（﹣，2+），P3（﹣，2﹣）．
综上所述：使得以A、C、P为顶点的三角形是等腰三角形，点P的坐标（﹣，0），（﹣，2+），（﹣，2﹣）．
