Question

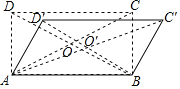
【题目】如图，矩形木框ABCD中，AB＝2AD＝4，将其按顺时针变形为ABC′D′，当∠AD′B＝90°时，四边形对称中心O经过的路径长为（　　）

A.B.C.D.

Answer 1

【答案】D

【解析】

取AB的中点E，连接EO，EO′．根据三角形中位线定理证明EO=1，由题意可知O的运动轨迹是以E为圆心的弧，求出圆心角，利用弧长公式计算即可.

如图，取AB的中点E，连接EO，EO′．

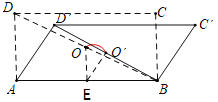
在Rt△AD′B中，∵∠AD′B＝90°，AB＝2AD，

∴cos∠BAD′＝，

∴∠BAD′＝60°，

∵AE＝EB，D′O＝O′B

∴O′E//AD′,

∴∠O′EB=∠BAD′＝60°

∵四边形ABCD是矩形，

∴∠BAD＝90°，

∵AE＝EB，DO＝OB，

∴OE＝AD＝1，OE//AD

∠OEB=∠BAD＝90°

∴∠OEO′=∠OEB-∠O′EB=30°，

∴点O的运动轨迹是以E为圆心的弧，

∴四边形对称中心O经过的路径长为．

故选：D．