题目内容
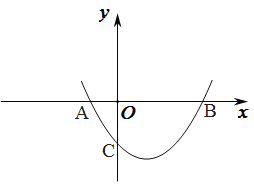
【题目】如图，抛物线y=x2+bx+c与x轴交于A(-1，0)，B(3，0)两点。
（1）求b、c的值；
（2）P为抛物线上的点，且满足S△PAB=8，求P点的坐标
（3）设抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小?若存在，求出Q点的坐标；若不存在，请说明理由。
【答案】（1）b=-2，c=-3；（2）符合x的值为点P有三个；（3）Q点的坐标为（1，-2）
【解析】
（1）抛物线y=x2+bx+c与x轴的两个交点分别为A（-1，0），B（3，0），把它们分别代入得到二元一次方程组，解这个方程组求得b，c值；
（2）设点P的坐标为（x，y），根据S△PAB=8，列出方程求得y值，分别代入从而求得点P的坐标；
（3）由AC长为定值，要使△QAC的周长最小，只需QA+QC最小．由几何知识可知，Q是直线BC与对称轴x=1的交点，再求得BC的直线解析式，从而求得点Q的坐标．
（1）根据题意可得，1-b+c=0；9+3b+c=0
∴b=-2，c=-3
∴抛物线的解析式为：y=x2-2x-3.
（2）设点P的坐标为（x，y）
根据题意可知，S△PAB=
×4|y|=8，∴|y|=4，∴y=±4
当y=4时，x2-2x-3=4，∴x=
或x=-
+1
当y=-4时，x2-2x-3=-4，∴x=1
∴当P点的坐标分别为(，4)、(-+1，4)、（1，-4）时，
S△PAB=8；
（3）在抛物线y=x2-2x-3的对称轴上存在点Q，使得△QAC的周长最小．
∵AC长为定值，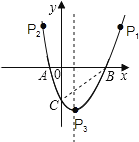
∴要使△QAC的周长最小，只需QA+QC最小．
∵点A关于对称轴x=1的对称点是B（3，0），
∴由几何知识可知，Q是直线BC与对称轴x=1的交点，
抛物线y=x2-2x-3与y轴交点C的坐标为（0，-3），设直线BC的解析式为y=kx-3．
∵直线BC过点B（3，0），
∴3k-3=0，
∴k=1．
∴直线BC的解析式为y=x-3，
∴当x=1时，y=-2．
∴点Q的坐标为（1，-2）．
