题目内容
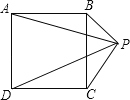
【题目】如图，正方形ABCD外有一点P，P在BC外侧，并在平行线AB与CD之间，若PA＝
，PB＝
，PC＝
，则PD＝（ ）
A.2B.
C.3D.
【答案】A
【解析】
用EF，BE，AB分别表示AP，BP，用CF，PF，DC分别表示DP，CP，得AP2+CP2=DP2+BP2，已知AP，BP，CP代入上式即可求DP．
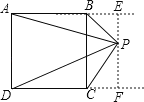
解：延长AB，DC，过P分作PE⊥AE，PF⊥DF，则CF＝BE，
AP2＝AE2+EP2，BP2＝BE2+PE2，
DP2＝DF2+PF2，CP2＝CF2+FP2，
∴AP2+CP2＝CF2+FP2+AE2+EP2，
DP2+BP2＝DF2+PF2+BE2+PE2，
即AP2+CP2＝DP2+BP2，
代入AP，BP，CP得DP＝
.
故选：A．
练习册系列答案
相关题目
