题目内容
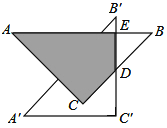
【题目】如图,在△ABC中,AB=4,AC=2,BC=5,点I为△ABC的内心,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
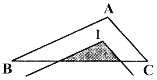
A.4B.5C.6D.7
【答案】B
【解析】
连接AI、BI,因为三角形的内心是角平分线的交点,所以AI是∠CAB的平分线,由平行的性质和等角对等边可得:AD=DI,同理BE=EI,所以图中阴影部分的周长就是边AB的长.
解:连接BI、CI,
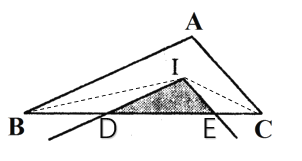
∵点I为△ABC的内心,
∴BI平分∠ABC,
∴∠ABI=∠CBI,
由平移得:AB∥DI,
∴∠ABI =∠BID,
∴∠CBI =∠BID,
∴BD=DI,
同理可得:CE=EI,
∴△DIE的周长=DE+DI+EI=DE+BD+CE=BC=5,
即图中阴影部分的周长为5,
故选:B.

练习册系列答案
相关题目
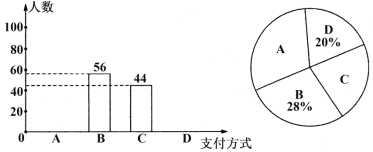
【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?