题目内容
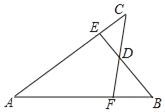
【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.


【答案】(1)理由见解析;(2)当点E在射线BC上移动5 s或2 s时,CF=AB.
【解析】试题分析:(1)、根据同角的余角相等得出答案;(2)、首先根据题意画出两个不同的图形,然后根据三角形全等得出线段的长度,从而得出运动的时间.
试题解析:(1)因为∠A+∠ACD=90°,∠BCD+∠ACD=90°, 所以∠A=∠BCD.
(2)如图,当点E在射线BC上移动时,若点E移动5 s,则BE=2×5=10(cm),
所以CE=BE-BC=10-3=7(cm). 所以CE=AC.
在△CFE与△ABC中,  所以△CFE≌△ABC, 所以CF=AB.
所以△CFE≌△ABC, 所以CF=AB.
当点E在射线CB上移动时,若点E移动2 s,则BE'=2×2=4(cm),
所以CE'=BE'+BC=4+3=7(cm), 所以CE'=AC.
在△CF'E'与△ABC中,  所以△CF'E'≌△ABC. 所以CF'=AB.
所以△CF'E'≌△ABC. 所以CF'=AB.
总之,当点E在射线BC上移动5 s或2 s时,CF=AB.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]() ,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
,承包商应如何选种树苗才能获得最大利润?最大利润是多少?