题目内容
已知反比列函数y=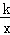
的图象在每一条曲线上，y都随x的增大而增大，
（1）求k的取值范围；
（2）在曲线上取一点A，分别向x轴、y轴作垂线段，垂足分别为B、C，坐标原点为O，若四边形ABOC面积为12，求此函数的解析式．
（1）k＜0 （2）y=﹣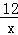
解析试题分析：（1）直接根据反比例函数的性质求解即可，k＜0；
（2）直接根据k的几何意义可知：过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，所以|k|=12，而k＜0，则k=﹣12．
解：（1）∵反比列函数y=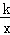的图象在每一条曲线上，y都随x的增大而增大，
∴k＜0；
（2）设A（x，y），由已知得，|xy|=|k|=12，
∵k＜0，
∴k=﹣12，
所以，反比例函数的解析式为y=﹣．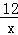
点评：主要考查了反比例函数中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
的图象与反比例函数
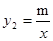的图象的两个交点是A（－2，－4），C（4，n），与y轴交于点B，与x轴交于点D．
交AB，BC分别于点M，N，反比例函数
的图象经过点M，N．
（k≠0）和一次函数y=x﹣6．
的图象是由反比例函数
的图象向左平移2个单位长度得到．灵活运用这一知识解决问题．
的图象C与正比例函数y=ax（a≠0）的图象l相交于点A（2，2）和点B．
的解集．
（x≠﹣1）的图象在第一象限内的交点为P（x0，3）．
