题目内容
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,求证EG=BE+GD.

(2)请用(1)的经验和知识完成此题:如图2,在四边形ABCD中,AG//BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
【答案】(1)证明见解析;(2)EG=10.
【解析】
(1)延长AD至F,使DF=BE,连接CF,根据正方形的性质,可直接证明△EBC≌△FDC,从而得出∠BCE=∠DCF,根据∠GCE=45°,得∠GCF=∠GCE=45°,利用全等三角形的判定方法得出△ECG≌△FCG,即GE=GF,即可证出EG=BE+GD;
(2)过C作CD⊥AG,交AG延长线于D,则四边形ABCD是正方形,设EG=x,则AE=8,根据(1)可得:AG=16-x,在直角△ADE中利用勾股定理即可求解.
(1)证明:如图3所示,延长AD至F,使DF=BE,连接CF,
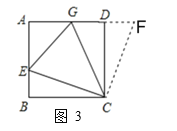
∵四边形ABCD是正方形,
∴BC=DC,∠ABC=∠ADC=∠BCD=90°,
∵∠CDF=180°-∠ADC,
∴∠CDF=90°,
∴∠ABC=∠CDF,
∵BE=DF,
∴△EBC≌△FDC,
∴∠BCE=∠DCF,EC=FC,
∵∠ECG=45°,
∴∠BCE+∠GCD=90°-∠ECG=90°-45°=45°,
∴∠GCD+∠DCF=∠FCG=45°,
∴∠ECG=∠FCG.
∵GC=GC,EC=FC,
∴△ECG≌△FCG,
∴EG=GF.
∵GF=GD+DF= BE+GD,
∴EG= BE+GD.
(2)解:如图4,过C作CD⊥AG,交AG延长线于D,

在直角梯形ABCD中,
∵AG∥BC,∠A=∠B=90°,
又∠CDA=90°,AB=BC,
∴四边形ABCD为正方形.
∴AD=AB=BC=12.
已知∠ECG=45°,根据(1)可知,EG=BE+DG,
设EG=x,则AG=AD-DG= AD-(EG-BE)=12-(x-4)=16-x,
∴AE=12-BE=12-4=8.
在Rt△AEG中
∵EG2=AG2+AE2,
即x2=(16-x)2+82,
解得:x=10.
∴EG=10.

【题目】在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 59 | 96 |
| 295 | 480 | 601 |
摸到白球的频率 |
| 0.64 | 0.58 | 0.59 | 0.60 | 0.601 |
(1)上表中的![]() ________,
________,![]() ________;
________;
(2)“摸到白球的”的概率的估计值是_________(精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?



