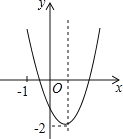题目内容
【题目】已知二次函数![]() .
.
(1)将二次函数化成顶点式为 ;
(2)当 时,![]() 随
随![]() 的增大而减小;
的增大而减小;
(3)当![]() 时,
时,![]() 的取值范围是 ;
的取值范围是 ;
(4)不等式![]() 的解集为 .
的解集为 .
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 或
或![]()
【解析】
(1)把二次函数y=x2-4x-5化为顶点式即可;
(2)根据二次函数的性质即可得到结论;
(3)把x=-3或x=1分别代入y=x2-4x-5,即可得到结论;
(4)解方程得到抛物线与x轴的解得坐标为(-1,0)和(5,0),即可得到结论.
(1)将二次函数化成y=x2-4x-5顶点式为y=(x-2)2-9;
(2)∵a=1>0,
∴抛物线的开口向上,
∵抛物线的对称轴为x=2,
∴当x<2时,y随x的增大而减小;
(3)把x=-3或x=1分别代入y=x2-4x-5得,y=16或y=-8,
∴当-3≤x≤1时,y的取值范围是-8≤y≤16;
(4)当y=0时,即x2-4x-5=0,
解得:x1=5,x2=-1,
∴抛物线与x轴的解得坐标为(-1,0)和(5,0),
不等式x2-4x-5>0的解集为x<-1或x>5,
故答案为:(1)y=(x-2)2-9;(2)x<2;(3)-8≤y≤16;(4)x<-1或x>5.

【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
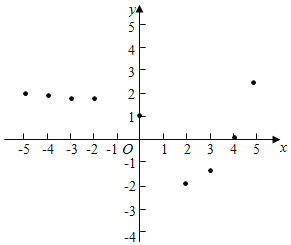
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .