题目内容
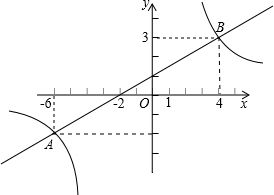 如图所示,一次函数y=kx+b的图象与反比例函数y=
如图所示,一次函数y=kx+b的图象与反比例函数y=| m | x |
(1)根据图象,求出两函数解析式;
(2)根据图象回答:当x为何值时,一次函数的函数值大于反比例函数的函数值;
(3)连结OA、OB,求△AOB的面积.
分析:(1)首先根据图象可以知道A、B的坐标,然后分别代入然两个函数解析式中利用待定系数法即可求解;
(2)结合图象可以直观的得到一次函数的函数值大于反比例函数的函数值图象上就是一次函数在反比例函数的上面,由此即可求解;
(3)△AOB的面积=△AOC的面积+△BOC的面积,根据三角形面积公式即可求解.
(2)结合图象可以直观的得到一次函数的函数值大于反比例函数的函数值图象上就是一次函数在反比例函数的上面,由此即可求解;
(3)△AOB的面积=△AOC的面积+△BOC的面积,根据三角形面积公式即可求解.
解答:解:(1)由图象可知:点A(-6,-2)、点B(4,3),
∵直线y=kx+b过A(-6,-2)、B(4,3)两点,
∴
,
解得
.
故一次函数的解析式为y=
x+1,
又∵反比例函数y=
的图象过点A(-6,-2)
∴m=12.
故反比例函数的解析式为y=
.
故两函数的解析式分别为y=
x+1和y=
;
(2)由图象得:当-6<x<0或x>4时,一次函数的函数值大于反比例函数的函数值;
(3)设直线y=
x+1与x轴的交点为C,则点C(-2,0).
∵△AOB的面积=△AOC的面积+△BOC的面积
∴△AOB的面积=
×|-2|×|-2|+
×|-2|×3=5.
∵直线y=kx+b过A(-6,-2)、B(4,3)两点,
∴
|
解得
|
故一次函数的解析式为y=
| 1 |
| 2 |
又∵反比例函数y=
| m |
| x |
∴m=12.
故反比例函数的解析式为y=
| 12 |
| x |
故两函数的解析式分别为y=
| 1 |
| 2 |
| 12 |
| x |
(2)由图象得:当-6<x<0或x>4时,一次函数的函数值大于反比例函数的函数值;
(3)设直线y=
| 1 |
| 2 |
∵△AOB的面积=△AOC的面积+△BOC的面积
∴△AOB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了一次函数和反比例函数的交点问题,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
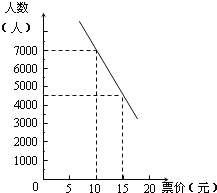 确保每周4万元的门票收入,那么每周应限定参观人数是多少门票价格应是多少元?
确保每周4万元的门票收入,那么每周应限定参观人数是多少门票价格应是多少元?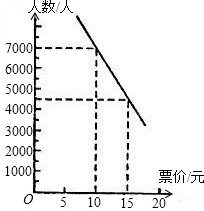

 某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,则旅客可携带的免费行李的最大质量为
某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,则旅客可携带的免费行李的最大质量为 某航空公司规定,旅客乘机所携带行李的运费y(元)与其质量x(kg)由(如图所示)一次函数确定,那么旅客可携带的免费行李的最大质量为( )
某航空公司规定,旅客乘机所携带行李的运费y(元)与其质量x(kg)由(如图所示)一次函数确定,那么旅客可携带的免费行李的最大质量为( )