题目内容
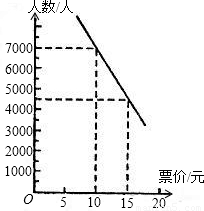
某博物馆每周都有大量中外游客前来参观,如果游客过多,则不利于博物馆中的一些珍贵文物的保存,但又需要一定量的门票收入用于解决文物的保存,保护等费用问题,因此博物馆通过浮动门票价格的方法来控制参观人数,调查统计发现,每周参观的人数与票价之间的关系可近似地看成如图所示的一次函数关系.(1)求图中一次函数的解析式;
(2)为确保每周4万元的门票收入,则门票价格应定为多少元?
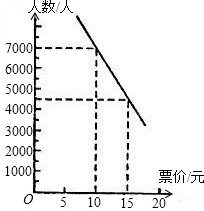
分析:(1)从图中可看出,一次函数经过点(10,7000)和点(15,4500),使用待定系数法列出方程组求解即可.
(2)由题意知,xy=40000,列出方程求得两根,由于游客过多不利于博物馆中的一些珍贵文物的保存,所以应舍去大根.
(2)由题意知,xy=40000,列出方程求得两根,由于游客过多不利于博物馆中的一些珍贵文物的保存,所以应舍去大根.
解答:解:(1)设一次函数的解析式为y=kx+b,
依题意
,
解得:
∴y=-500x+12000; (3分)
(2)xy=40000
即x(-500x+12000)=40000,
-x2+24x-80=0,
∵y=-500x+12000,k=-500<0
∴y随x的增大而减小
∴x=20
∴y=-500×20+12000=2000
答:门票价格应定为每人20元. (6分)
依题意
|
解得:
|
∴y=-500x+12000; (3分)
(2)xy=40000
即x(-500x+12000)=40000,
-x2+24x-80=0,
∵y=-500x+12000,k=-500<0
∴y随x的增大而减小
∴x=20
∴y=-500×20+12000=2000
答:门票价格应定为每人20元. (6分)
点评:考查学生对函数图象掌握情况及利用待定系数法求一次函数关系式,并结合实际情况对方程的根进行取舍.

练习册系列答案
相关题目