题目内容
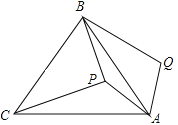
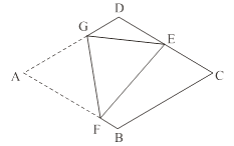
【题目】如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于于点P.

(1)求证:△ACE ≌ △BCD.
(2)求∠AOB的度数.
(3)连接OC,求证:OC平分∠AOD
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)利用等边三角形的性质证明![]() ;
;
(2)由![]() 得到∠CBD=∠CAE.再利用三角形内角和等于180°,由△APC和△BPO中有内角互为对顶角进而得出∠BOA=∠ACP=60°.
得到∠CBD=∠CAE.再利用三角形内角和等于180°,由△APC和△BPO中有内角互为对顶角进而得出∠BOA=∠ACP=60°.
(3)过C点作CG⊥AE,CH⊥BD,由三角形全等可得其对应高相等.再根据到角两边距离相等的点在角平分线即可得出结论.
(1)证明:![]() 与
与![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
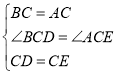 ,
,
![]() (SAS).
(SAS).
(2)![]() .
.
∴∠CBD=∠CAE,
∵∠BPO =∠APC,
又∵∠CBD+∠BPO+∠BOP=∠CAE+∠APC+∠ACP=180°.
∴∠BOP=∠ACP=60°,即∠AOB=60°.
(3)如图,过C点作CG⊥AE,CH⊥BD,
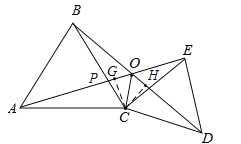
![]() ,
,
∴![]() ,AE=BD,
,AE=BD,
∴![]() ,
,
∴CG=CH,
又∵CG⊥AE,CH⊥BD,
∴OC是∠AOD的角平分线,即OC平分∠AOD.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目