题目内容
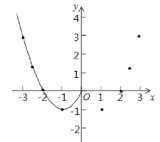
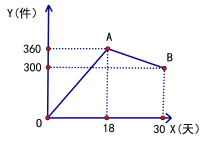
【题目】某商城经销一款新产品,该产品的进价6元/件,售价为9元/件.工作人员对30天销售情况进行跟踪记录并绘制成图象,图中的折线OAB表示日销售量![]() (件)与销售时间
(件)与销售时间![]() (天)之间的函数关系.
(天)之间的函数关系.
(1)第18天的日销售量是 件
(2)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围
的取值范围
(3)日销售利润不低于900元的天数共有多少天?
【答案】(1)360;(2)y=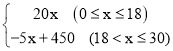 ;(3)16天
;(3)16天
【解析】
(1)根据图象即可得到结论;
(2)根据点的坐标,利用待定系数法可求出直线OA、AB的函数关系式,即可找出y与x之间的函数关系式;
(3)根据日销售量=日销售利润÷每件的利润,可求出日销售量,将其分别代入OA、AB的函数关系式中求出x值,将其相减加1即可求出日销售利润不低于900元的天数.
解:(1)由图象知,第18天的日销售量是360件;
故答案为:360;
(2)当![]() 时,设直线OA的函数解析式为:y=kx,
时,设直线OA的函数解析式为:y=kx,
把(18,360)代入得360=18k,
解得:k=20,
∴y=20x(0≤x≤18),
当18<x≤30时,设直线AB的函数解析式为:y=mx+n,
把(18,360),(30,300)代入得:![]() ,
,
解得:![]() ,
,
∴直线AB的函数解析式为:y=-5x+450,
综上所述,y与x之间的函数关系式为:y=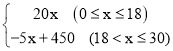 ;
;
(3)当 0≤x≤18 时,根据题意得,(9-6)×20x≥900,解得:x≥15;
当 18<x≤30 时,根据题意得,(9-6)×(-5x+450)≥900,解得:x≤30.
∴15≤x≤30;
∴30-15+1=16(天),
∴日销售利润不低于 900 元的天数共有 16天.

【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个) 的变化如下表:同时,销售过程中的其他开支(不含进价)总计40万元.
销售价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)观察并分析表中的数据,用所学过的函数知识,直接写出y与 x的函数解析式;
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格 x(元/个) 的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请你结合函数图象求出销售价格 x(元/个) 的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元 ?