题目内容
【题目】滨海新区某中学为了了解学生每周在校体育锻炼的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了不完整的统计图表，请根据图表信息解答下列问题
时间（小时） | 频数（人数） | 百分比 |
2≤t＜3 | 4 | 10% |
3≤t＜4 | 10 | 25% |
4≤t＜5 | a | 15% |
5≤t＜6 | 8 | b% |
6≤t＜7 | 12 | 30% |
合计 | 40 | 100% |
（1）表中的a＝ ，b＝ ；
（2）请将频数分布直方图补全；
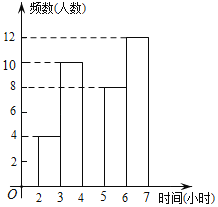
（3）若绘制扇形统计图，时间段6≤x＜7所对应扇形的圆心角的度数是多少？
（4）若该校共有1200名学生，估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名？
【答案】（1）6、20；（2）补全频数分布直方图见解析；（3）时间段6≤x＜7所对应扇形的圆心角的度数是108°；（4）估计全校每周在校参加体育锻炼时间至少有4小时的学生约为780名．
【解析】
(1)用总人数乘以所占的百分比即可求a，用b所对的频数除以总人数再乘以百分之百即可求得b;
(2)根据（1）中a的数据即可补全直方图；
(3)根据扇形图得到时间段
在扇形图中所占的百分比为30%，故可用30%乘以360°即可求得其所占的圆心角；
(4)已知在样本中锻炼至少有4小时所占的百分比为
，可根据样本估计总量，用全校总人数相乘即可.
（1）
，
，即
，
故答案为：6、20；
（2）补全频数分布直方图如下：
（3）时间段所对应扇形的圆心角的度数是
；
（4）估计全校每周在校参加体育锻炼时间至少有4小时的学生约为
（名）．
【题目】已知
、
在数轴上分别表示有理数
，
；
（1）对照数轴填写下表：
| 6 | -1 | -2 | 4 |
| 4 | -5 | 3 | -4 |
|
（2）若、两点间的距离记为
，试问：和，有何数量关系？
（3）写出所有符合条件的整数点
，使它到10和-10的距离之和为span>20，并求所有这些整数的数的和；
（4）找出（3）中满足到10和-10的距离之差大于1而小于5的整数的点；
（5）若点
表示的数为
，当点在什么位置时，
取得的值最小，并求出这个最小值.
