题目内容
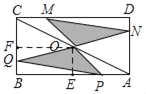
【题目】如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
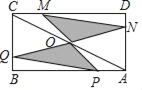
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
【答案】C
【解析】分析:过O作OE⊥AB于E,OF⊥BC于F,设BQ=x,由点P的速度是点Q的速度2倍,设AP=2x,BP=8﹣2x,CQ=4﹣x,用含x的代数式表示阴影部分的面积,根据函数的性质判断.
详解:如图所示,过O作OE⊥AB于E,OF⊥BC于F,
∵矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,
∴OE=![]() BC=2,OF=
BC=2,OF=![]() AB=4,
AB=4,
设BQ=x,则由点P的速度是点Q的速度2倍,可得AP=2x,BP=8﹣2x,CQ=4﹣x,
∵△POQ的面积=Rt△ABC的面积﹣△AOP的面积﹣△COQ的面积﹣△BPQ的面积
=![]() ×4×8﹣
×4×8﹣![]() ×2x×2﹣
×2x×2﹣![]() ×(4﹣x)×4﹣
×(4﹣x)×4﹣![]() x(8﹣2x)
x(8﹣2x)
=x2﹣4x+8,
∴阴影部分面积y=2x2﹣8x+16(0≤x≤4),
∴当x=2时,阴影部分面积y有最小值,
根据二次函数的性质,可得阴影部分面积先减小后增大,
故选C.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案【题目】滨海新区某中学为了了解学生每周在校体育锻炼的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了不完整的统计图表,请根据图表信息解答下列问题
时间(小时) | 频数(人数) | 百分比 |
2≤t<3 | 4 | 10% |
3≤t<4 | 10 | 25% |
4≤t<5 | a | 15% |
5≤t<6 | 8 | b% |
6≤t<7 | 12 | 30% |
合计 | 40 | 100% |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
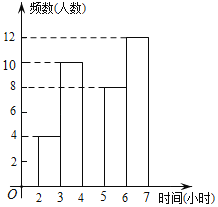
(3)若绘制扇形统计图,时间段6≤x<7所对应扇形的圆心角的度数是多少?
(4)若该校共有1200名学生,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?