题目内容
【题目】初步探究
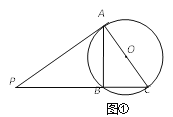
如图①,过点P的两条直线分别与⊙O相切于点A,与⊙O相交于B、C两点,且AC恰好经过圆心O.求证△PAB∽△PCA.
进一步探究
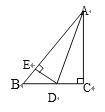
如图②若其他条件不变,但AC不经过圆心O.上述结论是否成立?请说明理由.

尝试应用
如图③,PA=3,PB=![]() ,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.
,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.

【答案】(1)证明见解析;(2)成立.理由见解析(3)1.
【解析】试题分析:(1)、根据切线的性质得出∠PAB+∠BAC=90°,根据直径的性质得出∠BAC+∠C=90°,从而得出∠PAB=∠C,结合公共角得出三角形相似;(2)、连接AO,延长AO交⊙O于D,连接BD,然后根据第一题相似的方法得出三角形相似;(3)、当AC为直径时以及三角形相似得出最短距离.
试题解析:(1)∵PA与⊙O相切, ∴∠PAC=90° ∴∠1+∠PAB=90°.
∵AC是⊙O的直径 ∴∠1+∠C=90° ∴∠PAB=∠C 又∵∠P=∠P ∴△PAB∽△PCA
(2)成立.连接AO,延长AO交⊙O于D,连接BD.
∵PA与⊙O相切 ∴∠PAD=90° ∴∠1+∠PAB=90° ∵AD是⊙O的直径
∴∠1+∠D=90° ∴∠PAB=∠D 又∵∠C=∠D ∴∠PAB=∠C
又∵∠P=∠P ∴△PAB∽△PCA.
(3)1.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目