题目内容
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结 CD,EB. 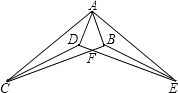
(1)不添加辅助线,找出图中其它的全等三角形;
(2)求证:CF=EF.
【答案】
(1)解:图中其它的全等三角形为:△ACD≌△AEB,△DCF≌△BEF
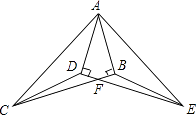
(2)证明:∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB﹣∠DAB=∠EAD﹣∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB,
∴CD=EB,∠ADC=∠ABE.
又∵∠ADE=∠ABC,
∴∠CDF=∠EBF.
又∵∠DFC=∠BFE,
∴△CDF≌△EBF(AAS).
∴CF=EF
【解析】(1)根据Rt△ABC≌Rt△ADE,得出AC=AE,BC=DE,AB=AD,∠ACB=∠AED,∠BAC=∠DAE,从而推出∠CAD=∠EAB,△ACD≌△AEB,△CDF≌△EBF;(2)先证得△CDF≌△EBF,进而得到CF=EF.
【考点精析】通过灵活运用全等三角形的性质,掌握全等三角形的对应边相等; 全等三角形的对应角相等即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目