题目内容
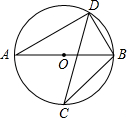
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.

(1)求证:D是BC的中点;
(2)求证:△BEC∽△ADC;
(3)若CE=5,BD=6.5,求AB的长.

(1)求证:D是BC的中点;
(2)求证:△BEC∽△ADC;
(3)若CE=5,BD=6.5,求AB的长.
(1)证明见解析; (2)证明见解析; (3)10.
试题分析:(1)根据圆周角定理的推论得到∠BDA=90°,再根据等腰三角形的性质即可得到BD=CD;
(2)根据有两对角相等的两个三角形相似证明即可;
(3)由(2)中的三角形相似可得到关于AC的比例式,AC可求,进而求出AB的长.
试题解析:(1)∵AB为⊙O的直径,∴∠BDA=90°.∴AD⊥BC.
∵AB=AC.∴BD=CD.∴D是BC的中点.
(2)∵AB=AC,∴∠C=∠ABD.
∵AB为⊙O的直径,∴∠ADB=∠BEC=90°.
∴△BEC∽△ADC.
(3)∵△BEC∽△ADC,∴CE:BD=BC:AC.
∵CE=5,BD=6.5,∴BC=2BD=13.
∴5:6.5=13:AC,∴AC=10.
∴AB=AC=10.

练习册系列答案
相关题目


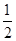 AB=
AB=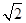 ,则半径OB的长为
,则半径OB的长为