��Ŀ����
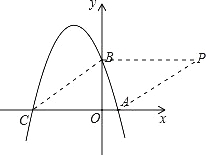
����Ŀ����֪��ͼ����ƽ��ֱ������ϵxOy�У���A��B��C�ֱ�Ϊ���������ϵ������㣬��OA=1��OB=3��OC=4��
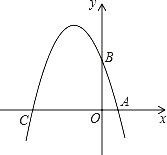
��1����A��B��C����������ߵĽ���ʽ��
��2����ƽ��ֱ������ϵxOy���Ƿ����һ��P��ʹ�����Ե�A��B��C��PΪ������ı���Ϊ���Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������MΪ����������һ���㣬�ڣ�2���������£��������|PM��AM|�����ֵʱ��M�����꣬��ֱ��д��|PM��AM|�����ֵ��
���𰸡���1��y=��![]() x2��
x2��![]() x+3����2����5��3������3����1��0������5����
x+3����2����5��3������3����1��0������5����![]() �������ֵΪ5.
�������ֵΪ5.
�������������������1���������ߵĽ���ʽΪy=ax2+bx+c����A��B��C��������������a��b��c��ֵ������ȷ�������������߽���ʽ����2����ƽ��ֱ������ϵxOy�д���һ��P��ʹ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�����Ϊ������OA��OB��OC�ij������ù��ɶ������BC��AC�ij���ȣ�ֻ�е�BP��ACƽ�������ʱ���ı���ACBPΪ���Σ��ɵó�BP�ij�����OB�ij�ȷ����P�������꣬ȷ����P���꣬����P�ڵڶ���������ʱ���Ե�A��B��C��PΪ������ı���ֻ����ƽ���ı��Σ��������Σ���3�����ô���ϵ����ȷ����ֱ��PA����ʽ������M���P��A����ͬһֱ����ʱ�����������ε����߹�ϵ|PM��AM|��PA������M���P��A��ͬһֱ����ʱ��|PM��AM|=PA������M���P��A��ͬһֱ����ʱ��|PM��AM|��ֵ�����MΪֱ��PA�������ߵĽ��㣬����ֱ��AP�������߽���ʽ�������|PM��AM|�����ֵʱM���꣬ȷ����|PM��AM|�����ֵ���ɣ�
�����������1���������ߵĽ���ʽΪy=ax2+bx+c�� ��A��1��0��B��0��3��C����4��0����
��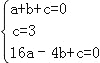 �� ��ã�a=��
�� ��ã�a=��![]() ��b=��
��b=��![]() ��c=3��
��c=3��
������A��B��C����������ߵĽ���ʽΪy=��![]() x2��
x2��![]() x+3��
x+3��
��2����ƽ��ֱ������ϵxOy�д���һ��P��ʹ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�����Ϊ��
��OB=3��OC=4��OA=1�� ��BC=AC=5�� ��BPƽ���ҵ���ACʱ���ı���ACBPΪ���Σ�
��BP=AC=5���ҵ�P��x��ľ������OB�� ����P������Ϊ��5��3����
����P�ڵڶ���������ʱ���Ե�A��B��C��PΪ������ı���ֻ����ƽ���ı��Σ��������Σ�
��P������Ϊ��5��3��ʱ���Ե�A��B��C��PΪ������ı���Ϊ���Σ�
��3����ֱ��PA�Ľ���ʽΪy=kx+b��k��0���� ��A��1��0����P��5��3����
��![]() �� ��ã�k=
�� ��ã�k=![]() ��b=��
��b=��![]() �� ��ֱ��PA�Ľ���ʽΪy=
�� ��ֱ��PA�Ľ���ʽΪy=![]() x��
x��![]() ��
��
����M���P��A����ͬһֱ����ʱ�����������ε����߹�ϵ|PM��AM|��PA��
����M���P��A��ͬһֱ����ʱ��|PM��AM|=PA��
������M���P��A��ͬһֱ����ʱ��|PM��AM|��ֵ�����MΪֱ��PA�������ߵĽ��㣬
�ⷽ����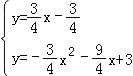 ����
����![]() ��
��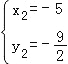 ��
��
����M������Ϊ��1��0������5����![]() ��ʱ��|PM��AM|��ֵ���ʱ|PM��AM|�����ֵΪ5��
��ʱ��|PM��AM|��ֵ���ʱ|PM��AM|�����ֵΪ5��