Question

【题目】如图，矩形的两条边分别在轴和轴上，已知点、点.

(1)若把矩形沿直线折叠，使点落在点处，直线与的交点分别为，求折痕的长；

(2)在(1)的条件下，点在轴上，在平面内是否存在点，使以为顶点的四边形是菱形？若存在，则请求出点的坐标；若不存在，请说明理由；

(3)如图，若为边上的一动点，在上取一点，将矩形绕点顺时针旋转一周，在旋转的过程中，的对应点为，请直接写出的最大值和最小值.

Answer 1

【答案】(1)折痕的长为；(2)点坐标为或或或；(3)的最小值为,的最大值为5.

【解析】

(1)连接AD，根据矩形的性质可求出，继而得，设，则，在中，根据勾股定理求出DC长，继而在中利用勾股定理求出DF长，证明，由全等三角形的性质得EF=DF，进而可求得答案；

(2)分两咱情形分别讨论即可：DE为菱形的边；DE为菱形的对角线；

(3)由题意点M在如图3中的圆环内或两个圆上，利用图象法即可解决问题.

(1)连接AD，

四边形是矩形，，

，

由折叠可得：，设，则，

在中，，

即 ，

解得 ，即，

在中， 即，

解得，

四边形是矩形，，

，

，

折痕的长为；

(2)由(1)可知，，

①当为菱形的边时，，可得，

②当为菱形的对角线时，与重合，与重合，，

③当点在第三象限，与关于轴对称，，

综上所述，点坐标为或或或；

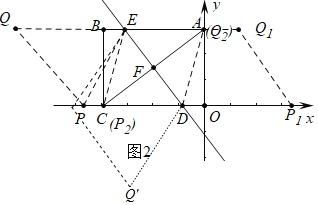
(3)如图中，作则，

观察图形可知，的最小值 ，

的最大值 .