题目内容
【题目】你知道古代数学家怎样解一元二次方程吗?以x2﹣2x﹣3=0为例,大致过程如下:第一步:将原方程变形为x2﹣2x=3,即x(x﹣2)=3.
第二步:构造一个长为x,宽为(x﹣2)的长方形,长比宽大2,且面积为3,如图所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图所示.
第四步:计算大正方形面积用x表示为 .长方形面积为常数 .小正方形面积为常数 .
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程 ,两边开方可求得:x1=3,x2=﹣1.
(1)第四步中横线上应填入 ; ; ; .
(2)请参考古人的思考过程,画出示意图,写出步骤,解方程x2﹣x﹣1=0.

【答案】(1)![]() ; 3 ; 4 ;
; 3 ; 4 ;![]() .(2)答案见解析.
.(2)答案见解析.
【解析】
(1)根据题意先表示出大正方形的边长再根据正方形的面积公式即可得出大正方形面积;
根据题意先得出小正方形的边长,再根据大正方形面积等于四个长方形与小正方形面积之和,即可得出答案;
(2)先将原方程变形,构造出一个长为x,宽为(x-1)的长方形,长比宽大1,且面积为1,再用四个这样的长方形围成一个大正方形,中间是一个小正方形,然后根据大正方形面积等于四个长方形与小正方形面积之和,得出一个方程,两边开方,即可求出方程的解.
(1)∵大正方形的边长是[x+(x-2)],
∴大正方形面积是:[x+(x-2)]2=(2x-2)2;
∵小正方形的边长是:[x+(x-2)]-2(x-2)=2,长方形的面积为3,
又∵大正方形面积等于四个长方形与小正方形面积之和,
∴(2x-2)2=4×3+22=16;
第四步中横线上应填入![]() ; 3 ; 4 ;
; 3 ; 4 ;![]() .
.
(2)解:第一步:将原方程变形为x2﹣x=1,即x(x﹣1)=1.
第二步:构造一个长为x,宽为(x﹣1)的长方形,长比宽大1,且面积为1.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形.
第四步:计算大正方形面积用x表示为[x+(x-1)]2.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程[x+(x﹣1)]2=4×1+12,两边开方可求得:x1=![]() ,x2=
,x2=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】小明家2002年四个季度的用电量如下:
季度名称 | 用电量(单位:千瓦时) |
第一季度 | 250 |
第二季度 | 150 |
第三季度 | 400 |
第四季度 | 200 |
其中各种电器用电量如下表:
各种电器 | 用电量(单位:千瓦时) |
空调 | 250 |
冰箱 | 400 |
照明 | 100 |
彩电 | 150 |
其他 | 100 |
小明根据上面的数据制成下面的统计图.
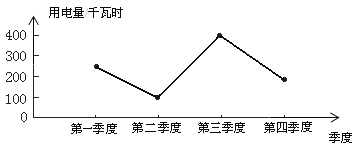
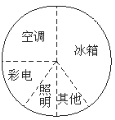
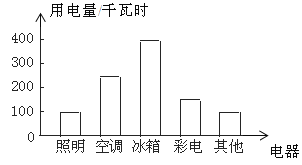
根据以上三幅统计图回答:
(1)从哪幅统计图中可以看出各个季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱用电量超过总用电量的![]() ?
?
(3)从哪幅统计图中可以清楚地看出空调的用电量?
【题目】在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出A、B两种园艺造型共50个,搭造要求的花盆数如下表所示:
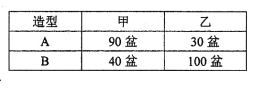
请问符合要求的搭造方案有几种?请写出具体的方案。
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备用体育用品 | 篮球 | 排球 | 羽毛球拍 |
单位(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?若能,求出篮球、排球、羽毛球拍各购买多少件;若不能,请说明理由.