题目内容
李明投资销售一种进价为20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500.
⑴设李明每月获得利润为W(元),当销售单价定为多少元时,每月获得利润最大?(4分)⑵如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3分)⑶根据物价部门规定,这种护眼台灯不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)(3分)
⑴设李明每月获得利润为W(元),当销售单价定为多少元时,每月获得利润最大?(4分)⑵如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3分)⑶根据物价部门规定,这种护眼台灯不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)(3分)
(1) 35 (2)30或40 (3)3600
解:(1)利用每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500,则可得到利润函数l=(-10x+500)(x-20),结合二次函数的性质可知。
(2)中利用2000=(-10x+500)(x-20),解得x=30或40 (3)中,利用成本=进价×销售量得到关系式,结合每月获得的利润不低于2000元,护眼台灯不得高于32元可得。
(2)中利用2000=(-10x+500)(x-20),解得x=30或40 (3)中,利用成本=进价×销售量得到关系式,结合每月获得的利润不低于2000元,护眼台灯不得高于32元可得。

练习册系列答案
相关题目

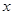 分钟,上网费用为
分钟,上网费用为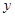 元.
元.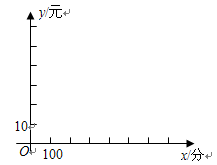
 和
和 的图象相交于点(-1,-2),则关于x的
的图象相交于点(-1,-2),则关于x的 >
> 的解集为( )
的解集为( )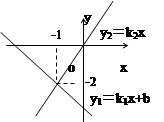
 =
=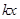 +
+ ,当
,当 的值增大1时,
的值增大1时,