题目内容
若一次函数 =
=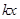 +
+ ,当
,当 的值增大1时,
的值增大1时, 值减小3,则当
值减小3,则当 的值减小3时,
的值减小3时, 值(*)
值(*)
 =
=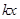 +
+ ,当
,当 的值增大1时,
的值增大1时, 值减小3,则当
值减小3,则当 的值减小3时,
的值减小3时, 值(*)
值(*)| A.增大3 | B.减小3 | C.增大9 ( | D.减小9 |
C
由题意得,当 的值增大1时,
的值增大1时, 值减小3,与则当
值减小3,与则当 的值减小3时构成两个相似三角形,且相似比为1:3,从而得出当
的值减小3时构成两个相似三角形,且相似比为1:3,从而得出当 的值减小3时,
的值减小3时, 值增大9
值增大9
故选C
 的值增大1时,
的值增大1时, 值减小3,与则当
值减小3,与则当 的值减小3时构成两个相似三角形,且相似比为1:3,从而得出当
的值减小3时构成两个相似三角形,且相似比为1:3,从而得出当 的值减小3时,
的值减小3时, 值增大9
值增大9故选C

练习册系列答案
相关题目
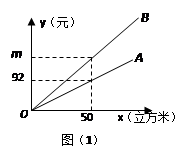
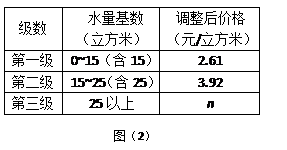

 )本, 则付款金额y(元)与练习本个数x(本)之间的函数关系式是 .
)本, 则付款金额y(元)与练习本个数x(本)之间的函数关系式是 . (元/件)
(元/件) (件)
(件)



 (k≠0)和
(k≠0)和 的图象大致是( )
的图象大致是( )