Question

【题目】已知△ABC，△EFG均是边长为4的等边三角形，点D是边BC、EF的中点． （Ⅰ）如图①，这两个等边三角形的高为；
（Ⅱ）如图②，直线AG，FC相交于点M，当△EFG绕点D旋转时，线段BM长的最小值是 ．

Answer 1

【答案】2 ；2 -2
【解析】解：（Ⅰ）如图①中，连接AD，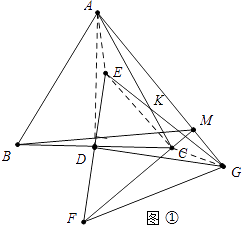
∵△ABC是等边三角形，BD=CD，
∴AD⊥BC，
在Rt△ABD中，∵AB=4，BD=2，
∴AD= = =2 ，
所以答案是2 ．
（Ⅱ）如图①中，连接AE、EC、CG．
∵DE=DF=DC，
∴△EFC是直角三角形，
∴∠ECF=90°，
∵∠ADC=∠EDG=90°，
∴∠ADE=∠GDC，
在△ADE和△GDC中，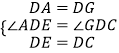
，
∴△ADE≌△GDC，
∴AE=CG，∠DAE=∠DGC，
∵DA=DG，
∴∠DAG=∠DGA，
∴∠GAE=∠AGC，
∵AG=GA，
∴△AGE≌△GAC，
∴∠GAK=∠AGK，
∴KA=KG，∵AC=EG，
∴EK=KC，
∴∠KEC=∠KCE，
∵∠AKG=∠EKC，
∴∠KAG=∠KCE，
∴EC∥AG，
∴∠AMF=∠ECF=90°，
∴点M在以AC为直径的圆上运动，
如图②中，当点M运动到BM⊥AC时，BM最短，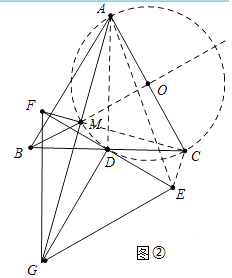

∵OB=2 ，AO=OM=OC=2，
∴BM的最小值为2 ﹣2．
所以答案是2 ﹣2．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对旋转的性质的理解，了解①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．