题目内容
【题目】将直角边长为6的等腰直角△AOC放在平面直角坐标系中，点O为坐标原点，点C、A分别在x轴，y轴的正半轴上，一条抛物线经过点A、C及点B（﹣3，0）．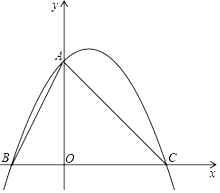
（1）求该抛物线的解析式；
（2）若点P是线段BC上一动点，过点P作AB的平行线交AC于点E，连接AP，当△APE的面积最大时，求点P的坐标；
（3）若点P（t，t）在抛物线上，则称点P为抛物线的不动点，将（1）中的抛物线进行平移，平移后，该抛物线只有一个不动点，且顶点在直线y=2x﹣ 
上，求此时抛物线的解析式．
【答案】
（1）
解：∵B（﹣3，0），C（6，0），设抛物线为y=a（x+3）（x﹣6），过A（0，6）
∴6=a（0+3）（0﹣6），
解得a=﹣ 
，
∴y=﹣ （x+3）（x﹣6），
即y=﹣ x2+x+6；
（2）
解：设P（m，0），
如图，
∵PE∥AB，
∴△PCE∽△BCA，
∴ 
，
，
∴S△PCE= 
，
∴S=S△APC﹣S△PCE=﹣ m2+m+6，
=﹣ （m﹣ 
）2+ 
，
∴当m= 时，S有最大值为 ；
∴P（ ，0）
（3）
解：设平移后的抛物线的顶点为G（h，k），
∴抛物线解析式为y=﹣ （x﹣h）2+k，
由抛物线的不动点的定义，得，t=﹣ （t﹣h）2+k，
即：t2+（3﹣2h）t+h2﹣3k=0，
∵平移后，抛物线只有一个不动点，
∴此方程有两个相等的实数根，
∴△=（3﹣2h）2﹣4（h2﹣3k）=0，
∴h﹣k= 
①，
∵顶点在直线y=2x﹣ 
上，
∴k=2k﹣ ②，
∴联立①②得，h=1，k= 
，
∴抛物线的解析式为y=﹣ （x﹣1）2+ =﹣ x2+ 
x﹣ 
【解析】（1）已知抛物线与x轴的两个交点坐标，所以设抛物线方程为两点式：y=a（x+3）（x﹣6），然后把点A的坐标代入该函数解析式即可求得系数a的值；（2）利用相似三角形的性质得出S△PCE= ，进而求出△APE的面积S，即可得出点P坐标；（3）利用抛物线上不动点的定义以及不动点的个数得出方程h﹣k= ①，再用平移后的抛物线的顶点在直线y=2x﹣ 上，得出方程k=2k﹣ ②，联立解方程组即可．
【考点精析】本题主要考查了抛物线与坐标轴的交点和相似三角形的判定的相关知识点，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）才能正确解答此题．
