题目内容
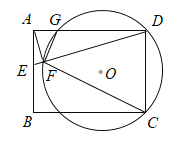
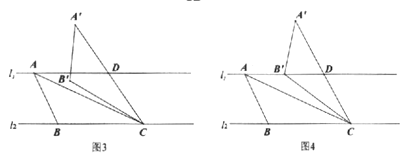
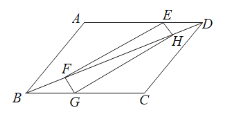
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
【答案】![]()
【解析】
根据菱形的性质得到AD∥BC,得到∠GBF=∠EDH,可证明△BGF≌△DEH(AAS),得到BG=DE;连接GE,过点G作GQ//AB,交AD于点P,过点E作EQ⊥GQ,垂足为Q,证明四边形ABGP为平行四边形,得到AP=BG=2,∠GPE=120°,求得PE=2,∠EPQ=60°,进而求得PQ=1,QE=![]() ,运用勾股定理求得GE的长,从而可得FH的长.
,运用勾股定理求得GE的长,从而可得FH的长.
∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
∵DE=2,
∴BG=2;
过点G作GQ//AB,交AD于点P,过点E作EQ⊥GQ,垂足为Q,如图,
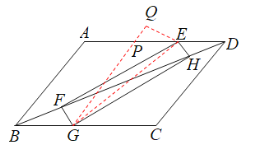
则四边形ABGP是平行四边形,
∴AP=BG=2,GP=AB=6,∠GPE=∠A=120°,
∴∠EPQ=60°,PE=AD-AP-DE=6-2-2=2
在Rt△PQE中 , ∠EPQ=60°,PE=2
∴∠QEP=30°,
∴QP=1
∴![]()
在Rt△GQE中,∠GQE=90°,GQ=GP+PQ=6+1=7,
∴![]()
∵四边形EFGH是矩形,
∴FH=GE=![]() .
.
故答案为:![]() .
.

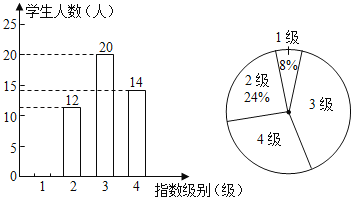
【题目】为弘扬祖国优秀传统文化,加强优秀文化熏陶,提高学生的文化素养和道德素质,我县某校举行了“经典启迪人生,国学伴我成长”主题活动,学校统一印制独具本校特色的国学教育校本教材,通过课堂教学和课外活动相结合的方式进行国学教育,为了解学生学习成果,现随机抽取了部分同学的国学成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.调查结果扇形统计图.
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 50≤x<60 | 40 | 0.10 |
B | 60≤x<70 | 60 | c |
C | 70≤x<80 | a | 0.20 |
D | 80≤x<90 | 160 | 0.40 |
E | 90≤x<100 | 60 | 0.15 |
合计 | b | 1 |
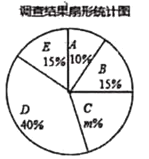
(1)根据以上信息解答问题:(1)统计表中a=________,b= ________,c=_______.
(2)扇形统计图中,m的值为________,“D”所对应的圆心角的度数是_______度;
(3)若参加国学教育的同学共有2000人,请你估计成绩在90分及以上的学生大约有多少人?
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.