题目内容
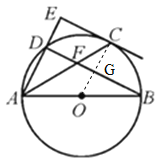
【题目】如图,AB为⊙O的直径,C、D两点均在⊙O上,过点C作CE⊥AD于点E,且AC平分∠BAD.
(1)求证:CE为⊙O的切线;
(2)连结BD交AC于点F,若CF=5,sin∠CAD=![]() ,求线段BD的长.
,求线段BD的长.

【答案】(1)见解析;(2) ![]() .
.
【解析】分析:(1)连结OC交BD于点G.证明∠ECA+∠ACO=90°即可得到结论;
(2)设DF=3x,则AF=5x,AD=4x.由∠CAD=∠ACO,得到sin∠FCG=![]() .进而表示出BG,OG,OB.在Rt△OBG中,由勾股定理得到OB2=OG2+BG2,解方程即可得出结论.
.进而表示出BG,OG,OB.在Rt△OBG中,由勾股定理得到OB2=OG2+BG2,解方程即可得出结论.
详解:(1)连结OC交BD于点G.
∵AC平分∠BAD,∴∠CAD=∠CAB.
又∵OA=OC,∴∠CAB=∠ACO.
又∵CE⊥AD, ∴∠E=90°,∴∠EAC+∠ECA=90°,
∴∠ECA+∠ACO=90°,∴CE为⊙O的切线.
(2)设DF=3x,则AF=5x,AD=4x.
又∵AB为⊙O的直径,∴∠ADB=90°,∴BD∥CE,∴OC⊥BD.
又∵∠CAD=∠ACO,∴sin∠FCG=![]() .
.
又∵CF=5,∴CG=4,FG=3,∴DG=BG=3x+3.
又∵OC∥AE,∴OG=![]() AD=2x,∴OC=OB=4+2x.
AD=2x,∴OC=OB=4+2x.
在Rt△OBG中,OB2=OG2+BG2,∴(4+2x)2=(2x)2+(3x+3)2 ,
∴x=![]() 或-1.
或-1.
又∵x>0,∴x=![]() ,∴BD=2BG=
,∴BD=2BG=![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目