题目内容
9. 如图,已知△ABC和△A′B′C′关于MN对称,并且AC=5,BC=2,A′B′=4,则△A′B′C′的周长是( )
如图,已知△ABC和△A′B′C′关于MN对称,并且AC=5,BC=2,A′B′=4,则△A′B′C′的周长是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 根据对称的性质可得出A′C′=AC=5、B′C′=BC=2,再结合A′B′=4利用三角形的周长公式即可求出结论.
解答 解:∵△ABC和△A′B′C′关于MN对称,
∴A′C′=AC=5,B′C′=BC=2,
∵A′B′=4,
∴△A′B′C′的周长为A′C′+B′C′+A′B′=5+2+4=11.
故选C.
点评 本题考查了轴对称的性质,根据△ABC和△A′B′C′关于MN对称找出A′C′=AC、B′C′=BC、A′B′=AB是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
1.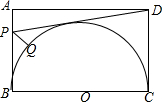 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )| A. | 5 | B. | $\sqrt{13}$+2 | C. | $\frac{\sqrt{73}}{2}$+$\frac{1}{2}$ | D. | 3$\sqrt{5}$-2 |
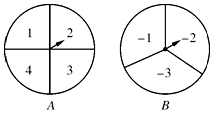 如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止. 如图,已知在?ABCD中,AE平分∠BAD,即∠1=∠2,BF平分∠ABC,即∠3=∠4,连接EF,求证:四边形ABEF是菱形.
如图,已知在?ABCD中,AE平分∠BAD,即∠1=∠2,BF平分∠ABC,即∠3=∠4,连接EF,求证:四边形ABEF是菱形.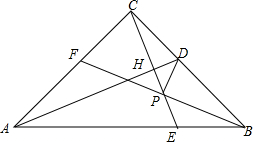 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )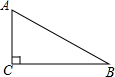 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.用直尺和圆规,作出点D的位置.(不写作法,保留作图痕迹)
如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.用直尺和圆规,作出点D的位置.(不写作法,保留作图痕迹)