题目内容
如图,已知反比例函数 (x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)写出反比例函数解析式;
(2)求证:∆ACB∽∆NOM;
(3)若∆ACB与∆NOM的相似比为2,求出B点的坐标及AB所在直线的解析式.

 (x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.(1)写出反比例函数解析式;
(2)求证:∆ACB∽∆NOM;
(3)若∆ACB与∆NOM的相似比为2,求出B点的坐标及AB所在直线的解析式.

(1)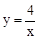 ;(2)证明见解析;(3)
;(2)证明见解析;(3)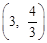 ,
,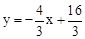 .
.
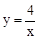 ;(2)证明见解析;(3)
;(2)证明见解析;(3)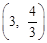 ,
,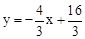 .
.试题分析:(1)根据点在曲线上点的坐标满足方程的关系,将点A的坐标代入
 即可求出k,从而得到反比例函数解析式.
即可求出k,从而得到反比例函数解析式.(2)由于∠ACB =∠NOM = 90°,所以要证ΔACB∽ΔNOM,只要
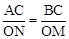 即可,由已知分别求出
即可,由已知分别求出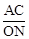 和
和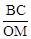 ,证明它们相等即可.
,证明它们相等即可.(3)由ΔACB与ΔNOM的相似比为2,根据(2)相似比为
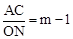 ,列式求解即可得到点B的坐标,从而应用待定系数法即可求得AB所在直线的解析式.
,列式求解即可得到点B的坐标,从而应用待定系数法即可求得AB所在直线的解析式.试题解析:(1)∵
 的图象经过点A(1,4),∴
的图象经过点A(1,4),∴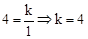 .
.∴反比例函数解析式为
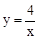 .
.(2)∵ B(m,n),A(1,4),∴AC = 4–n,BC = m–1,ON = n,OM = 1.
∴
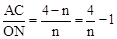 .
.∵点B(m,n)在
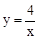 上,∴
上,∴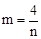 . ∴
. ∴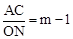 .
.又∵
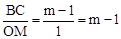 . ∴
. ∴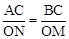 .
.又∵∠ACB =∠NOM = 90°,∴ ΔACB∽ΔNOM..
(3)∵ ΔACB与ΔNOM的相似比为2,∴m–1 =" 2." ∴m = 3.
∴B点坐标为
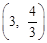 .
.设AB所在直线的解析式为y = kx+b,
∴
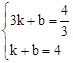 ,解得
,解得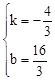 .
.∴AB所在直线的解析式为
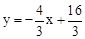 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 与直线
与直线 交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程
交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程 的解为
的解为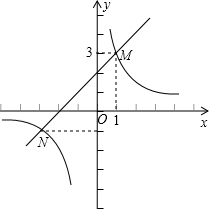
 的图像分别是
的图像分别是 ,半径为1的
,半径为1的 与直线
与直线 中的两条相切,例如
中的两条相切,例如 是其中一个
是其中一个
 与
与 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① ;②
;② ;③当
;③当 时,
时, 中,正确的个数是 ( )
中,正确的个数是 ( )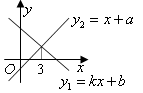
 随着所处深度
随着所处深度 的变化而变化,在某个地点
的变化而变化,在某个地点 来表示,则
来表示,则 的图象如图所示,下列结论正确的是
的图象如图所示,下列结论正确的是