题目内容
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )
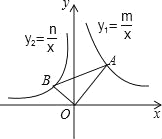
A.m=![]() nB.m=﹣
nB.m=﹣![]() nC.m=﹣
nC.m=﹣![]() nD.m=﹣3n
nD.m=﹣3n
【答案】D
【解析】
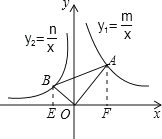
过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,设点B坐标为(a,![]() ),点A的坐标为(b,
),点A的坐标为(b,![]() ),证明△BOE∽△OAF,利用对应边成比例可求出m、n的关系.
),证明△BOE∽△OAF,利用对应边成比例可求出m、n的关系.
过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,
∵∠OAB=30°,
∴OA=![]() ,
,
设点B坐标为(a, ![]() ),点A的坐标为(b,
),点A的坐标为(b, ![]() ),
),
则OE=a,BE=![]() ,OF=b,AF=
,OF=b,AF=![]() ,
,
∵∠BOE+∠OBE=90°,∠AOF+∠BOE=90°,
∴∠OBE=∠AOF,
又∵∠BEO=∠OFA=90°,
∴△BOE∽△OAF,
∴![]() ,即
,即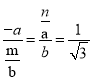 ,
,
解得:m![]() ,n=
,n=![]() ,
,
故可得:m=3n.
故选:D.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:
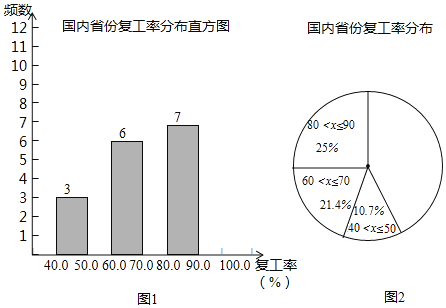
a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.