题目内容
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交
轴交 ![]() 、
、 ![]() 两点,直线
两点,直线 ![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.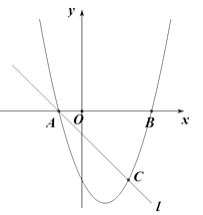
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 ![]() 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
【答案】
(1)解:将A(﹣1,0),B(3,0)代入 ![]() ,
,
得b=﹣2,c=3;
∴ ![]() .
.
将C点的横坐标x=2代入 ![]() ,
,
得y=-3,
∴C(2,-3);
∴直线AC的函数解析式是y=﹣x﹣1
(2)解:设P点的横坐标为x(﹣1≤x≤2),
则P、E的坐标分别为:P(x,﹣x﹣1),E(x, ![]() );
);
∵P点在E点的上方,PE=(﹣x﹣1)﹣( ![]() )=
)= ![]() ,
,
∴当x= ![]() 时,PE的最大值为
时,PE的最大值为 ![]()
【解析】(1)利用待定系数法,把A、B坐标代入解析式即可;(2)解决最值问题的基本策略是函数思想,构建以P点的横坐标x为自变量,PF长为因变量的函数,再利用配方法求出最值.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.

练习册系列答案
相关题目
【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 36 | 52 |
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?





