题目内容
【题目】在平面直角坐标系中,点![]() 为坐标原点,已知点
为坐标原点,已知点![]() ,将
,将![]() 绕坐标原点
绕坐标原点![]() 旋转90°到
旋转90°到![]() ,则点
,则点![]() 的坐标是__________.
的坐标是__________.
【答案】![]() 或
或![]()
【解析】
根据题意作图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,根据旋转的性质可得OA=OA′,利用同角的余角相等求出∠OAB=∠A′OB′,然后利用“角角边”证明△AOB和△OA′B′全等,根据全等三角形对应边相等可得OB′=AB,A′B′=OB,然后写出点A′的坐标,同理求出逆时针旋转90![]() 时A′的坐标,故可求解.
时A′的坐标,故可求解.
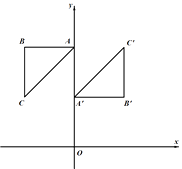
如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,

∵OA绕坐标原点O顺时针旋转90![]() 至OA′,
至OA′,
∴OA=OA′,∠AOA′=90![]() ,
,
∵∠A′OB′+∠AOB=90![]() ,∠AOB+∠OAB=90
,∠AOB+∠OAB=90![]() ,
,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
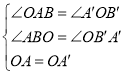 ,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(4,3).
同理OA绕坐标原点O逆时针旋转90![]() 至OA′
至OA′
OB’=AB=4,A’B’=OB=3
∴点A′的坐标为(-4,3).
综上,点A′的坐标为(4,3)或(-4,3).
故答案为:![]() 或
或![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目