题目内容
【题目】如图,PA、PB切⊙O于A、B, ![]() ,点C是⊙O上异于A、B的任意一点,则
,点C是⊙O上异于A、B的任意一点,则 ![]() = .
= . 
【答案】65°或115°
【解析】分两种情况:(1)当C在优弧AB上;(2)当C在劣弧AB上;连接OA、OB,在四边形PAOB中,∠OAP=∠OBP=90°,由内角和求得∠AOB的大小,然后根据圆周角定理即可求得答案(1)如图(1),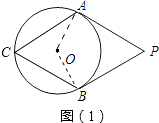
连接OA、OB.
在四边形PAOB中,由于PA、PB分别切⊙O于点A、B,
则∠OAP=∠OBP=90°;
由四边形的内角和定理,知
∠APB+∠AOB=180°;
又∵∠P=50°,
∴∠AOB=130°;
又∵∠ACB= ![]() ∠AOB(同弧所对的圆周角是所对的圆心角的一半),
∠AOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠ACB=65°(2)如图(2),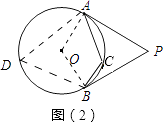
连接OA、OB,作圆周角∠ADB.
在四边形PAOB中,由于PA、PB分别切⊙O于点A、B,
则∠OAP=∠OBP=90°;
由四边形的内角和定理,知
∠APB+∠AOB=180°;
又∠P=50°,
∴∠AOB=130°;
∴∠ADB= ![]() ∠AOB=65°,
∠AOB=65°,
∴∠ACB=180°﹣∠ADB=115°.
∴∠ACB=65°或115°
【考点精析】通过灵活运用圆周角定理和圆内接四边形的性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.

练习册系列答案
相关题目