题目内容
①-89+100
②(-14)-(-16)
③(-4)×6
④(-63)÷(-7)
⑤(1-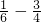 )×(-48)
)×(-48)
⑥-50÷2×(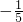 )
)
⑦|-3|-(-5)+(-6)+4
⑧-(1.5)-(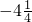 )+3.75-(
)+3.75-(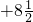 )
)
⑨-23+(-3)×-(-3)2÷(-2)
⑩-(3-5)+32×(1-3)
解:①原式=11;
②原式=-14+16,
=2;
③原式=-24;
④原式=9;
⑤原式=-(48- ×48-
×48- ×48),
×48),
=-(48-8-36),
=-4
⑥原式=-50× ×(
×(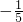 )
)
=5;
⑦原式=3+5-6+4.
=6;
⑧原式=-1.5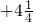 +3.75
+3.75
=-1.5-8 +8,
+8,
=-2
⑨原式=-8+(-3)×9÷(-2),
=-8+13.5,
=5.5
⑩原式=2+9×(-2),
=2-18,
=-16.
分析:①根据有理数的加法法则计算;
②根据有理数的加法法则计算;
③根据有理数的乘法法则计算就可以;
④运用有理数的除法法则计算;
⑤运用乘法分配律进行计算简便;
⑥根据有理数的乘除法一次计算就可以了;
⑦先去绝对值,再运用有理数的加减计算就可以了;
⑧先去括号,在运用加法的交换律和结合律进行简便运算;
⑨先进行乘方和乘除运算,在进行加减计算就可以了;
⑩先进行有理数的乘方和乘法运算,再进行乘法运算,最后进行加减运算就可以.
点评:本题考查了有理数的加法法则,有理数的加法法则,有理数的乘除法法则及乘方法则的运用,在解答的过程中注意结果符号的确定和运算顺序的确定.
②原式=-14+16,
=2;
③原式=-24;
④原式=9;
⑤原式=-(48-
 ×48-
×48- ×48),
×48),=-(48-8-36),
=-4
⑥原式=-50×
 ×(
×(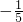 )
)=5;
⑦原式=3+5-6+4.
=6;
⑧原式=-1.5
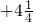 +3.75
+3.75
=-1.5-8
 +8,
+8,=-2
⑨原式=-8+(-3)×9÷(-2),
=-8+13.5,
=5.5
⑩原式=2+9×(-2),
=2-18,
=-16.
分析:①根据有理数的加法法则计算;
②根据有理数的加法法则计算;
③根据有理数的乘法法则计算就可以;
④运用有理数的除法法则计算;
⑤运用乘法分配律进行计算简便;
⑥根据有理数的乘除法一次计算就可以了;
⑦先去绝对值,再运用有理数的加减计算就可以了;
⑧先去括号,在运用加法的交换律和结合律进行简便运算;
⑨先进行乘方和乘除运算,在进行加减计算就可以了;
⑩先进行有理数的乘方和乘法运算,再进行乘法运算,最后进行加减运算就可以.
点评:本题考查了有理数的加法法则,有理数的加法法则,有理数的乘除法法则及乘方法则的运用,在解答的过程中注意结果符号的确定和运算顺序的确定.

练习册系列答案
相关题目
某校初二学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.请你回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
方差的公式为s2=
[(x1-x)2+(x2-x)2+…+(xn-x)2].
| ′ | 1号 | 2号 | 3号 | 4号 | 5号 | 总分 |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
方差的公式为s2=
| 1 |
| n |
某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
请你回答下列问题:
(1)计算两班的优秀率;
(2)分别求出两班比赛数据的平均数、中位数和两个班的方差;
(3)经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,来确定冠军奖.根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率;
(2)分别求出两班比赛数据的平均数、中位数和两个班的方差;
(3)经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,来确定冠军奖.根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
某校八年级学生开展踢毽子比赛,每班派5名学生参加,按团体总分高低排名次,成绩较好的甲、乙两班各5名学生的比赛成绩如下(单位:次)
甲班:100 98 110 89 103;乙班:89 100 95 119 97.
下表是整理后的一部分数据:
(1)把上表中所缺的数据补全(在规定时间内每人踢100次及100次以上为优秀);
(2)从平均数和中位数看, 班的成绩较好;
(3)从平均数和优秀率看, 班的成绩较好;
(4)从数据的波动程度看,估计 班的方差较小;
(5)根据以上信息,你认为应把冠军奖状发给 班.
甲班:100 98 110 89 103;乙班:89 100 95 119 97.
下表是整理后的一部分数据:
| 总次数 | 平均数 | 中位数 | 优秀率 | |
| 甲班 | 500 | 100 | ||
| 乙班 | 97 | 40% |
(2)从平均数和中位数看,
(3)从平均数和优秀率看,
(4)从数据的波动程度看,估计
(5)根据以上信息,你认为应把冠军奖状发给
为认真贯彻国家教育部等关于在中小学开展阳光体育运动的精神,加强体育锻炼,提高学生的身体素质,某校八年级学生在五月份开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定的时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据:(单位:个)
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其它数据作为参考.
请你回答下列问题:
(1)甲、乙两班的平均分分别为 、 .甲、乙两班的优秀率分别为、 .
(2)甲、乙两班比赛数据的中位数分别为 、 .
(3)甲、乙两班比赛数据的方差分别为 、 .(保留整数)
(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
| 班级 | 1号 | 2号 | 3号 | 4号 | 5号 | 总分 |
| 甲 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙 | 89 | 100 | 95 | 119 | 97 | 500 |
请你回答下列问题:
(1)甲、乙两班的平均分分别为
(2)甲、乙两班比赛数据的中位数分别为
(3)甲、乙两班比赛数据的方差分别为
(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
某校九年级学生在“五四”期间开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定的时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
请你运用所学过的统计知识,加以评判;你认为应该把冠军奖状发给哪个班级并说明理由.
请你运用所学过的统计知识,加以评判;你认为应该把冠军奖状发给哪个班级并说明理由.
| 班级 | 1号 | 2号 | 3号 | 4号 | 5号 | 合计 |
| 甲 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙 | 89 | 100 | 95 | 119 | 97 | 500 |