题目内容
某校初二学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):| ′ | 1号 | 2号 | 3号 | 4号 | 5号 | 总分 |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
方差的公式为s2=
| 1 |
| n |
分析:(1)优秀率等于100分以上(含100分)的人数除以总人数;
(2)按大小顺序排列,中间一个数或两个数的平均数为中位数;
(3)由方差的公式进行计算即可;
(4)根据比赛成绩的优秀率高,中位数大,方差小,综合评定,则甲班踢毽子水平较好.
(2)按大小顺序排列,中间一个数或两个数的平均数为中位数;
(3)由方差的公式进行计算即可;
(4)根据比赛成绩的优秀率高,中位数大,方差小,综合评定,则甲班踢毽子水平较好.
解答:解:(1)甲班的优秀率为:3÷5=0.6=60%,乙班的优秀率为:2÷5=0.4=40%;
(2)甲班5名学生比赛成绩的中位数是100个
乙班5名学生比赛成绩的中位数是97个;
(3)甲班的平均分为
=
=100,乙班的平均分为
=
=100,
甲班在这次比赛中的方差为:S甲2=
×[(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2=46.8,
乙班在这次比赛中的方差为:S乙2=
×[(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2
∴S甲2<S乙2;
(4)甲班定为冠军.因为甲班5名学生的比赛成绩的优秀率比乙班高,中位数比乙班大,方差比乙班小,综合评定甲班踢毽子水平较好.
(2)甲班5名学生比赛成绩的中位数是100个
乙班5名学生比赛成绩的中位数是97个;
(3)甲班的平均分为
. |
| x甲 |
| 500 |
| 5 |
. |
| x乙 |
| 500 |
| 5 |
甲班在这次比赛中的方差为:S甲2=
| 1 |
| 5 |
乙班在这次比赛中的方差为:S乙2=
| 1 |
| 5 |
∴S甲2<S乙2;
(4)甲班定为冠军.因为甲班5名学生的比赛成绩的优秀率比乙班高,中位数比乙班大,方差比乙班小,综合评定甲班踢毽子水平较好.
点评:本题考查了平均数,中位数,优秀率、方差的意义.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
请你回答下列问题:
(1)计算两班比赛数据的优秀率各是多少?;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差,并说明哪个班更稳定?
(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲班 | 101 | 97 | 110 | 90 | 102 |
| 乙班 | 90 | 100 | 95 | 118 | 97 |
(1)计算两班比赛数据的优秀率各是多少?;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差,并说明哪个班更稳定?
(4)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
某校初二学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
| ′ | 1号 | 2号 | 3号 | 4号 | 5号 | 总分 |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
方差的公式为
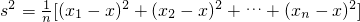 .
. 某校初二学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢l00个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总分相等.此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)分别计算两班的优秀率.
(2)分别求出两班比赛数据的中位数.
(3)分别计算两班比赛数据的方差并比较.
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.