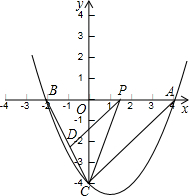题目内容
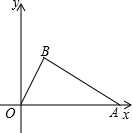
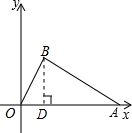
如图,己知Rt△OAB的斜边OA在x轴正半轴上,直角顶点B在第一象限,OA=5,OB=
.
(1)求A、B两点的坐标;
(2)求经过O、A、B三点且对称轴平行于y轴的抛物线的解析式,并确定抛物线顶点的坐标.
| 5 |
(1)求A、B两点的坐标;
(2)求经过O、A、B三点且对称轴平行于y轴的抛物线的解析式,并确定抛物线顶点的坐标.

(1)∵OA在x轴正半轴上,且OA=5,
∴A点坐标为(5,0);(1分)
过B作BD⊥OA于D,则△BOD∽△AOB,
∴
=
;
∴OD=
=1;
在Rt△ODB中,由勾股定理得,BD=
=2;
∴B点坐标为(1,2);(2分)
(2)因为抛物线经过O(0,0)、A(5,0)两点,
∴可设其解析式为y=ax(x-5);(3分)
又∵过点B(1,2),∴2=a(1-5)×1,
∴a=-
;(4分)
∴所求抛物线解析式为y=-
x(x-5),即y=-
x2+
x;(5分)
配方得y=-
(x-
)2+
;
∴抛物线顶点坐标为(
,
).(6分)
∴A点坐标为(5,0);(1分)
过B作BD⊥OA于D,则△BOD∽△AOB,
∴
| OB |
| OA |
| OD |
| OB |
∴OD=
| OB2 |
| OA |
在Rt△ODB中,由勾股定理得,BD=
| OB2-OD2 |
∴B点坐标为(1,2);(2分)
(2)因为抛物线经过O(0,0)、A(5,0)两点,
∴可设其解析式为y=ax(x-5);(3分)
又∵过点B(1,2),∴2=a(1-5)×1,
∴a=-
| 1 |
| 2 |
∴所求抛物线解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
配方得y=-
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
∴抛物线顶点坐标为(
| 5 |
| 2 |
| 25 |
| 8 |


练习册系列答案
相关题目

 过点A的直线y=x+c与x轴交于点N,与这个二次函数的图象交于点B.
过点A的直线y=x+c与x轴交于点N,与这个二次函数的图象交于点B.