Question

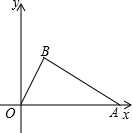
如图，已知二次函数y=

1

2

x²+bx+c的图象与x轴只有一个公共点M，与y轴的交点为A，过点A的直线y=x+c与x轴交于点N，与这个二次函数的图象交于点B．
（1）求点A、B的坐标（用含b、c的式子表示）；
（2）当S_△BMN=4S_△AMN时，求二次函数的解析式；
（3）在（2）的条件下，设点P为x轴上的一个动点，那么是否存在这样的点P，使得以P、A、M为顶点的三角形为等腰三角形？若存在，请写出符合条件的所有点P的坐标；若不存在，请说明理由．

Answer 1

（1）

y= 1 2 x2+bx+c(1) y=x+c(2)

x₁=0，x₂=2-2b
当x₁=0时，y₁=c即A（0，c）
当x₂=2-2b时，y₂=2-2b+c
即B（2-2b，2-2b+c）；

（2）2-2b-3c=0，△=0
得b²-2c=0，
联立③，④得
（6+2）（36-2）=0
∴b₁=-2，b₂=

2

3

-

b

2a

＞0，而a=

1

2

＞0．
∴b＜0．
∴b=-2
当b=-2时，代入④得c=2
∴所求二次函数的解析式为：y=

1

2

x²-2x+2；

（3）存在符合条件的点P
P_l（2+2

2

，0），P₂（0，0），P₃（2-2

2

，0），P₄（-2，0）．